如图,$ D$,$E $ 分别为 $ \triangle ABC $ 边 $ AB$,$AC $ 的中点,直线 $ DE $ 交 $ \triangle ABC $ 的外接圆于 $ F$,$G $ 两点.若 $ CF\parallel AB $,证明: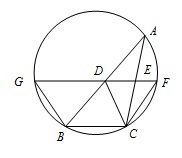

【难度】
【出处】
无
【标注】
-
$ CD=BC $;标注答案解析因为 $ D$,$E $ 分别为 $ AB$,$AC $ 的中点,所以 $ DE\parallel BC $.
又已知 $ CF\parallel AB $,故四边形 $ BCFD $ 是平行四边形,
所以 $ CF=BD=AD $.而 $ CF\parallel AD $,连接 $ AF $,
所以四边形 $ ADCF $ 是平行四边形,故 $ CD=AF $.
因为 $ CF\parallel AB $,所以 $ BC=AF $,故 $ CD=BC $.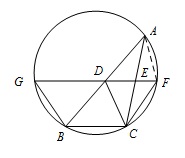
-
$ \triangle BCD \backsim \triangle GBD $.标注答案解析因为 $ FG\parallel BC $,故 $ GB=CF $.
由(1)可知 $ BD=CF $,所以 $ GB=BD $,所以 $ \angle{BGD}=\angle{BDG} $.
由 $ BC=CD $ 知 $\angle{CBD}=\angle{CDB} $,
而 $ \angle DGB=\angle EFC=\angle DBC $,
故 $ \triangle BCD \backsim \triangle GBD $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2