如图，$A,B,C,D$ 四点在同一圆上，$AD$ 的延长线与 $BC$ 的延长线交于 $E$ 点，且 $EC = ED$．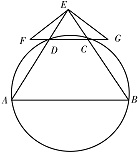
【难度】
【出处】
无
【标注】
-
证明：$CD\parallel AB$；标注答案解析$EC = ED$，所以\[\angle EDC = \angle ECD.\]因为 $A,B,C,D$ 四点在同一圆上，所以\[\angle EDC = \angle EBA.\]故\[\angle ECD = \angle EBA.\]所以 $CD\parallel AB$．
-
延长 $CD$ 到 $F$，延长 $DC$ 到 $G$，使得 $EF = EG$，证明：$A,B,G,F$ 四点共圆．标注答案解析由（1）知，$AE = BE$，因为 $EF = EG$，故\[\angle EFD = \angle EGC,\]从而\[\angle FED = \angle GEC.\]连结 $AF,BG$，
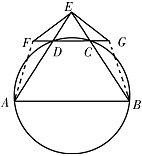则 $\triangle EFA \cong \triangle EGB$，故\[\angle FAE = \angle GBE.\]又 $CD\parallel AB$，$\angle EDC = \angle ECD$，所以\[\angle FAB = \angle GBA.\]由（1）中结论 $CD\parallel AB$ 可得 $\angle AFG+\angle FAB=180^\circ$，所以\[\angle AFG + \angle GBA = 180^\circ .\]故 $A,B,G,F$ 四点共圆．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
