已知正方体 $ABCD - A'B'C'D'$ 中,点 $ M $ 是棱 $AA'$ 的中点,点 $O$ 是对角线 $BD'$ 的中点.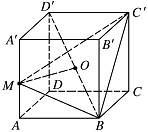

【难度】
【出处】
2010年高考四川卷(文)
【标注】
-
求证:$ OM $ 为异面直线 $AA'$ 与 $BD'$ 的公垂线;标注答案解析法一:
如图,连结 $ AC $,取 $ AC中 $ 点 $ K $,则 $ K $ 为 $ BD $ 的中点,连结 $ OK $.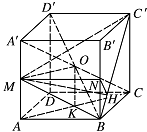 因为 $ M $ 是棱 $ AA' $ 的中点,点 $ O $ 是 $ BD' $ 的中点.
因为 $ M $ 是棱 $ AA' $ 的中点,点 $ O $ 是 $ BD' $ 的中点.
所以 $ AM \parallel DD'\parallel OK $,$ AM =\dfrac{1}{2}DD'=OK $,所以 $AKOM$ 为平行四边形.
所以 $ MO \parallel AK $,$ MO = AK $.
由 $ AA'\perp AK $,得 $ MO\perp AA' $,
因为 $ AK\perp BD $,$ AK\perp BB' $,所以 $ AK\perp 平面BDD'B' $,
所以 $ AK\perp BD' $,所以 $ MO\perp BD' $.
又因为 $ OM $ 是异面直线 $ AA' $ 和 $ BD' $ 都相交,
故 $ OM $ 为异面直线 $ AA' $ 和 $ BD' $ 的公垂线.
法二:
设正方体棱长为 $ 1 $.以点 $ D $ 为坐标原点,建立如图所示空间直角坐标系 $ D-xyz $.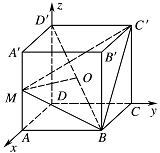 则\[A\left(1,0,0\right) , B\left(1,1,0\right) , C\left(0,1,0\right) , A'\left(1,0,1\right) , C'\left(0,1,1\right) , D'\left(0,0,1\right) .\]因为点 $M$ 是棱 $AA'$ 的中点,点 $O$ 是 $BD'$ 的中点.
则\[A\left(1,0,0\right) , B\left(1,1,0\right) , C\left(0,1,0\right) , A'\left(1,0,1\right) , C'\left(0,1,1\right) , D'\left(0,0,1\right) .\]因为点 $M$ 是棱 $AA'$ 的中点,点 $O$ 是 $BD'$ 的中点.
所以 $M\left(1,0, \dfrac{1}{2} \right)$,$O\left( \dfrac{1}{2},\dfrac{1}{2}, \dfrac{1}{2} \right)$,所以\[\overrightarrow {OM} = \left(\dfrac{1}{2}, - \dfrac{1}{2},0\right),\overrightarrow {AA'} =\left(0,0,1\right),\overrightarrow {BD'} =\left(-1,-1,1\right),\]所以\[\overrightarrow {OM} \cdot\overrightarrow {AA'} =0,\overrightarrow {OM} \cdot\overrightarrow {BD'} = - \dfrac{1}{2} + \dfrac{1}{2} +0=0.\]所以 $OM\perp AA'$,$OM\perp BD'$.
又因为 $OM$ 与异面直线 $AA'$ 和 $BD'$ 都相交,
故 $OM$ 为异面直线 $AA'$ 和 $BD'$ 的公垂线. -
求二面角 $M - BC' - B'$ 的大小.标注答案解析解法一:
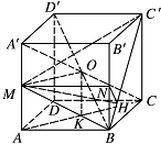 取 $ BB' $ 中点 $ N $,连结 $ MN $,则 $ MN\perp 平面BCC'B' $,
取 $ BB' $ 中点 $ N $,连结 $ MN $,则 $ MN\perp 平面BCC'B' $,
过点 $ N $ 作 $ NH\perp BC' $ 于 $ H $,连结 $ MH $,则由三垂线定理得 $ BC'\perp MH $.
从而 $ \angle MHN $ 为二面角 $ M-BC'-B' $ 的平面角,所以\[ MN=1 , NH=BN \sin 45^\circ = \dfrac{1}{2}\times\dfrac{{\sqrt 2 }}{2} = \dfrac{{\sqrt 2 }}{4} ,\]在 $ {\mathrm{Rt}}\triangle MNH $ 中,$ \tan \angle MHN= \dfrac{{MN}}{{NH}} = \dfrac{1}{{\dfrac{{\sqrt 2 }}{4}}} = 2\sqrt 2 $.
故二面角 $ M-BC'-B' $ 的大小为 $ \arctan 2 \sqrt 2 $.
解法二: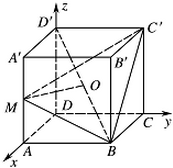 设平面 $ BMC' $ 的一个法向量为 $\overrightarrow {{n_1}} =\left(x,y,z\right)$,$\overrightarrow {BM} =\left(0,-1, \dfrac{1}{2}\right)$,$\overrightarrow {BC'} =\left(-1,0,1\right)$,
设平面 $ BMC' $ 的一个法向量为 $\overrightarrow {{n_1}} =\left(x,y,z\right)$,$\overrightarrow {BM} =\left(0,-1, \dfrac{1}{2}\right)$,$\overrightarrow {BC'} =\left(-1,0,1\right)$,
则\[\begin{cases}
\overrightarrow {{n_1}} \cdot\overrightarrow {BM} = 0 ,\\
\overrightarrow {{n_1}} \cdot\overrightarrow {BC'} = 0 ,\\
\end{cases}\]即\[\begin{cases}- y + \dfrac{1}{2}z = 0 ,\\
- x + z = 0 ,\\
\end{cases}\]取 $ z=2 $,则 $ x=2 $,$ y=1 $,从而 $\overrightarrow {{n_1}} =\left(2,1,2\right)$.
取平面 $ BC'B' $ 的一个法向量为 $\overrightarrow {{n_2}} =\left(0,1,0\right)$,所以\[\cos \left \langle \overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \right\rangle = \dfrac{{\overrightarrow {{n_1}} \cdot\overrightarrow {{n_2}} }}{{ \left|\overrightarrow {{n_1}} \right|\cdot \left|\overrightarrow {{n_2}} \right|}} = \dfrac{1}{{\sqrt 9 \cdot 1}} = \dfrac{1}{3}.\]由图可知,二面角 $ M-BC'-B' $ 的平面角为锐角,
故二面角 $ M-BC'-B' $ 的大小为 $ \arccos \dfrac{1}{3} $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2