（i）证明两角和的余弦公式 ${{\mathrm{C}}_{\left(\alpha + \beta\right) }}:\cos \left(\alpha + \beta \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $；
（ii）由 ${{\mathrm{C}}_{\left(\alpha + \beta \right)}}$ 推导两角和的正弦公式 ${{\mathrm{S}}_{\left(\alpha + \beta\right) }}:\sin \left(\alpha + \beta \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $．
（ii）由 ${{\mathrm{C}}_{\left(\alpha + \beta \right)}}$ 推导两角和的正弦公式 ${{\mathrm{S}}_{\left(\alpha + \beta\right) }}:\sin \left(\alpha + \beta \right) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $．
【难度】
【出处】
2010年高考四川卷（文）
【标注】
【答案】
【解析】
（i）如图，在直角坐标系 $ xOy $ 内作单位圆 $ O $，并作出角 $ {\alpha} $、$ {\beta} $ 与 $ -{\beta} $，使角 $ {\alpha} $ 的始边为 $ Ox $，交 $ ⊙O $ 于点 $ P_{1} $，终边交 $ ⊙O $ 于 $ P_{2} $；角 $ {\beta} $ 的始边为 $ OP_{2} $，终边交 $ ⊙O $ 于 $ P_{3} $；角 $ -{\beta} $ 的始边为 $ OP_{1} $，终边交 $ ⊙O $ 于 $ P_{4} $．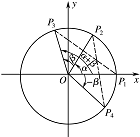
则\[ P_{1}\left(1,0\right) , P_{2}\left(\cos {\alpha} ,\sin {\alpha} \right) , P_{3}\left(\cos \left({\alpha} +{\beta} \right),\sin \left({\alpha} +{\beta} \right)\right) , P_{4}\left(\cos \left(-{\beta} \right),\sin \left(-{\beta} \right)\right) .\]由 $ P_{1}P_{3}=P_{2}P_{4} $ 及两点间的距离公式，得\[ \left[\cos\left({\alpha} +{\beta} \right)-1\right]^2+\sin^2\left({\alpha} +{\beta} \right)=\left[\cos \left(-{\beta} \right)-\cos{\alpha} \right]^2+\left[\sin\left(-{\beta} \right)-\sin{\alpha} \right]^2 ,\]展开并整理，得\[ 2-2\cos \left({\alpha} +{\beta} \right)=2-2\left(\cos {\alpha} \cos {\beta} -\sin {\alpha} \sin {\beta} \right), \]所以\[ \cos \left({\alpha} +{\beta} \right)=\cos {\alpha} \cos {\beta} -\sin {\alpha} \sin {\beta} .\]（ii）由（i）易得\[ \cos\left( \dfrac{{\mathrm{\pi }}}{2} -{\alpha} \right) =\sin {\alpha} , \sin\left( \dfrac{{\mathrm{\pi }}}{2}-{\alpha} \right) =\cos {\alpha} . \]及\[\begin{split}
\sin\left(α+β\right)&=\cos\left[ \dfrac{{\mathrm{\pi }}}{2} -\left(α+β\right)\right]\\ &=\cos\left[\left( \dfrac{{\mathrm{\pi }}}{2}-α\right)+\left(-β\right)\right]\\&=\cos\left( \dfrac{{\mathrm{\pi }}}{2} -α\right)\cos\left(-β\right)-\sin\left( \dfrac{{\mathrm{\pi }}}{2} -α\right)\sin\left(-β\right)\\&=\sin α\cos β+\cos α \sin β, \end{split}\]所以 $\sin\left({\alpha} +{\beta} \right)= \sin {\alpha} \cos {\beta} +\cos {\alpha} \sin {\beta} $．
则\[ P_{1}\left(1,0\right) , P_{2}\left(\cos {\alpha} ,\sin {\alpha} \right) , P_{3}\left(\cos \left({\alpha} +{\beta} \right),\sin \left({\alpha} +{\beta} \right)\right) , P_{4}\left(\cos \left(-{\beta} \right),\sin \left(-{\beta} \right)\right) .\]由 $ P_{1}P_{3}=P_{2}P_{4} $ 及两点间的距离公式，得\[ \left[\cos\left({\alpha} +{\beta} \right)-1\right]^2+\sin^2\left({\alpha} +{\beta} \right)=\left[\cos \left(-{\beta} \right)-\cos{\alpha} \right]^2+\left[\sin\left(-{\beta} \right)-\sin{\alpha} \right]^2 ,\]展开并整理，得\[ 2-2\cos \left({\alpha} +{\beta} \right)=2-2\left(\cos {\alpha} \cos {\beta} -\sin {\alpha} \sin {\beta} \right), \]所以\[ \cos \left({\alpha} +{\beta} \right)=\cos {\alpha} \cos {\beta} -\sin {\alpha} \sin {\beta} .\]（ii）由（i）易得\[ \cos\left( \dfrac{{\mathrm{\pi }}}{2} -{\alpha} \right) =\sin {\alpha} , \sin\left( \dfrac{{\mathrm{\pi }}}{2}-{\alpha} \right) =\cos {\alpha} . \]及\[\begin{split}\sin\left(α+β\right)&=\cos\left[ \dfrac{{\mathrm{\pi }}}{2} -\left(α+β\right)\right]\\ &=\cos\left[\left( \dfrac{{\mathrm{\pi }}}{2}-α\right)+\left(-β\right)\right]\\&=\cos\left( \dfrac{{\mathrm{\pi }}}{2} -α\right)\cos\left(-β\right)-\sin\left( \dfrac{{\mathrm{\pi }}}{2} -α\right)\sin\left(-β\right)\\&=\sin α\cos β+\cos α \sin β, \end{split}\]所以 $\sin\left({\alpha} +{\beta} \right)= \sin {\alpha} \cos {\beta} +\cos {\alpha} \sin {\beta} $．
答案
解析
备注
