如图,已知椭圆 ${C_1}$ 的中心在原点 $O$,长轴左、右端点 $M,N$ 在 $x$ 轴上,椭圆 ${C_2}$ 的短轴为 $MN$,且 ${C_1},{C_2}$ 的离心率都为 $e$.直线 $l \perp MN$,$l$ 与 ${C_1}$ 交于两点,与 ${C_2}$ 交于两点,这四点按纵坐标从大到小依次为 $A、B、C、D$.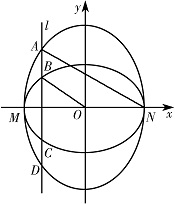

【难度】
【出处】
无
【标注】
-
设 $e = \dfrac{1}{2}$,求 $\left| {BC} \right|$ 与 $\left| {AD} \right|$ 的比值;标注答案解析因为 ${C_1},{C_2}$ 的离心率相同,故依题意可设\[\begin{split}{C_1}&:\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1(a>b>0), \\ {C_2}&:\dfrac{{{b^2}{y^2}}}{{{a^4}}} + \dfrac{{{x^2}}}{{{a^2}}} = 1,\end{split}\]设直线 $l: x = t \left( {\left| t \right| < a} \right)$,分别与 ${C_1}、{C_2}$ 的方程联立,求得\[A\left( {t,\dfrac{a}{b}\sqrt {{a^2} - {t^2}} } \right),B\left( {t,\dfrac{b}{a}\sqrt {{a^2} - {t^2}} } \right).\]当 $e = \dfrac{1}{2}$ 时,\[b = \dfrac{{\sqrt 3 }}{a}a,\]分别用 ${y_A}、{y_B}$ 表示 $A、B$ 的纵坐标,可知\[\left| {BC} \right|:\left| {AD} \right| = \dfrac{{2\left| {{y_B}} \right|}}{{2\left| {{y_A}} \right|}} = \dfrac{{{b^2}}}{{{a^2}}} = \dfrac{3}{4}.\]
-
当 $e$ 变化时,是否存在直线 $l$,使得 $BO\parallel AN$?并说明理由.标注答案解析$t = 0$ 时的 $l$ 不符合题意,
$t \ne 0$ 时,$BO\parallel AN$,当且仅当\[{k_{BO}}={k_{AN}},\]即\[\dfrac{{\dfrac{b}{a}\sqrt {{a^2} - {t^2}} }}{t} = \dfrac{{\dfrac{a}{b}\sqrt {{a^2} - {t^2}} }}{{t - a}},\]解得\[t = - \dfrac{{a{b^2}}}{{{a^2} - {b^2}}} = \dfrac{{1 - {e^2}}}{{{e^2}}} \cdot a,\]因为 $\left| t \right| < a$,且 $0 < e < 1$,所以\[\dfrac{{1 - {e^2}}}{{{e^2}}} < 1,\]解得\[\dfrac{{\sqrt 2 }}{2} < e < 1.\]综上,得
当 $0 < e \leqslant \dfrac{{\sqrt 2 }}{2}$ 时,不存在直线 $l$,使得 $BO\parallel AN$;
当 $\dfrac{{\sqrt 2 }}{2} < e < 1$ 时,存在直线 $l$,使得 $BO\parallel AN$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2