题目

查看数据源：599165b92bfec200011de83e

如图，由 $ M $ 到 $ N $ 的电路中有 $ 4 $ 个组件，分别标为 $ T_{1} $，$ T_{2} $，$ T_{3} $，$ T_{4} $，电流能通过 $ T_{1} $，$ T_{2} $，$ T_{3} $ 的概率都是 $ p $，电流能通过 $ T_{4} $ 的概率是 $ 0.9 $．电流能否通过各组件相互独立．已知 $ T_{1} $，$ T_{2} $，$ T_{3} $ 中至少有一个能通过电流的概率为 $ 0.999 $．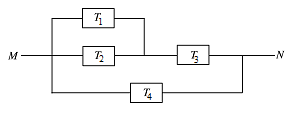

【难度】

【出处】

2010年高考大纲全国II卷（理）

【标注】

求 $ p $；
标注
答案

解析

记 $ A _i $ 表示事件：电流能通过 ${ T _i}$，$i = 1,2,3,4 $，
$ A $ 表示事件：${{ {T}}_1},{{{T}}_2},{{{T}}_3}$ 中至少有一个能通过电流，
由 $\overline A = \overline {{ A _1}} \cdot \overline {{ A _2}} \cdot \overline {{ A _3}}$，${ A _1},{ A _2},{ A _3}$ 相互独立，得\[\begin{split}P\left(\overline A \right)& = P\left(\overline {{A_1}} \cdot \overline {{A_2}} \cdot \overline {{A_3}} \right) \\&= P\left(\overline {{A_1}} \right)P\left(\overline {{A_2}} \right)P\left(\overline {{A_3}} \right) \\&= {\left(1 - p\right)^3} , \end{split}\]根据题意得\[\begin{split}P\left(\overline A \right) &= 1 - P\left(A\right) \\&= 1 - 0.999 = 0.001 ,\end{split}\]从而\[{\left(1 - p\right)^3} = 0.001,\]解得\[p = 0.9.\]
求电流能在 $ M $ 与 $ N $ 之间通过的概率；
标注
答案

解析

记 $ B $ 表示事件：电流能在 $ M $ 与 $ N $ 之间通过，则\[{B}={{{A}}_{{4}}}{+}\overline{{{{A}}_{{4}}}}\centerdot {{{A}}_{{1}}}\centerdot {{{A}}_{{3}}}{+}\overline{{{{A}}_{{4}}}}\centerdot \overline{{{{A}}_{{1}}}}\centerdot {{{A}}_{{2}}}\centerdot {{{A}}_{{3}}},\]所以\[ \begin{split} {P\left(B\right)} & =P\left({{{A}}_{{4}}}{+}\overline{{{{A}}_{{4}}}}\centerdot {{{A}}_{{1}}}\centerdot {{{A}}_{{3}}}+\overline{{{{A}}_{{4}}}}\centerdot \overline{{{{A}}_{{1}}}}\centerdot {{{A}}_{{2}}}\centerdot {{{A}}_{{3}}}\right) \\&
= P\left({{{A}}_{{4}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\centerdot {{{A}}_{{1}}}\centerdot {{{A}}_{{3}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\centerdot \overline{{{{A}}_{{1}}}}\centerdot {{{A}}_{{2}}}\centerdot {{{A}}_{{3}}}\right) \\&
=P\left({{{A}}_{{4}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\right)P\left({{{A}}_{{1}}}\right)P\left({{{A}}_{{3}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\right)P\left(\overline{{{{A}}_{{1}}}}\right)P\left({{{A}}_{{2}}}\right)P\left({{{A}}_{{3}}}\right)
\\& =0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9
=0.9891.\end{split}\]
$\xi $ 表示 $ T_{1} $，$ T_{2} $，$ T_{3} $，$ T_{4} $ 中能通过电流的组件个数，求 $\xi $ 的期望．
标注
答案

解析

由于电流能通过各元件的概率都是 $ 0.9 $，且电流能否通过各元件相互独立，
则 $\xi \sim B\left(4,0.9\right)$，从而 $E\xi = 4 \times 0.9 = 3.6$．

题目问题1 答案1 解析1 备注1 问题2 答案2 解析2

记 $ B $ 表示事件：电流能在 $ M $ 与 $ N $ 之间通过，则\[{B}={{{A}}_{{4}}}{+}\overline{{{{A}}_{{4}}}}\centerdot {{{A}}_{{1}}}\centerdot {{{A}}_{{3}}}{+}\overline{{{{A}}_{{4}}}}\centerdot \overline{{{{A}}_{{1}}}}\centerdot {{{A}}_{{2}}}\centerdot {{{A}}_{{3}}},\]所以\[ \begin{split} {P\left(B\right)} & =P\left({{{A}}_{{4}}}{+}\overline{{{{A}}_{{4}}}}\centerdot {{{A}}_{{1}}}\centerdot {{{A}}_{{3}}}+\overline{{{{A}}_{{4}}}}\centerdot \overline{{{{A}}_{{1}}}}\centerdot {{{A}}_{{2}}}\centerdot {{{A}}_{{3}}}\right) \\&<br/>= P\left({{{A}}_{{4}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\centerdot {{{A}}_{{1}}}\centerdot {{{A}}_{{3}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\centerdot \overline{{{{A}}_{{1}}}}\centerdot {{{A}}_{{2}}}\centerdot {{{A}}_{{3}}}\right) \\&<br/>=P\left({{{A}}_{{4}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\right)P\left({{{A}}_{{1}}}\right)P\left({{{A}}_{{3}}}\right)+P\left(\overline{{{{A}}_{{4}}}}\right)P\left(\overline{{{{A}}_{{1}}}}\right)P\left({{{A}}_{{2}}}\right)P\left({{{A}}_{{3}}}\right)<br/>\\& =0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9<br/>=0.9891.\end{split}\]