己知斜率为 $ 1 $ 的直线 $ l $ 与双曲线 $ C $:$\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\left( {a>0,b>0} \right)$ 相交于 $ B $、$ D $ 两点,且 $ BD $ 的中点为 $M\left( {1,3} \right)$.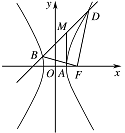

【难度】
【出处】
无
【标注】
-
求 $ C $ 的离心率;标注答案解析由题设知,$l$ 的方程为 $y = x + 2$.
代入 $ C $ 的方程,并化简,得\[\left({b^2} - {a^2}\right){x^2} - 4{a^2}x - 4{a^2} - {a^2}{b^2} = 0 .\]设 $B\left({x_1},{y_1}\right)$、$D\left({x_2},{y_2}\right)$,则\[ {x_1} + {x_2} = \dfrac{{4{a^2}}}{{{b^2} - {a^2}}},{x_1} \cdot {x_2} = - \dfrac{{4{a^2} + {a^2}{b^2}}}{{{b^2} - {a^2}}} , \quad \cdots \cdots ① \]由 $M\left(1,3\right)$ 为 $ BD $ 的中点知 $\dfrac{{{x_1} + {x_2}}}{2} = 1$,故 $\dfrac{1}{2} \times \dfrac{{4{a^2}}}{{{b^2} - {a^2}}} = 1$,
即\[{b^2} = 3{a^2} , \quad \cdots \cdots ② \]故 $c = \sqrt {{a^2} + {b^2}} = 2a$,所以 $ C $ 的离心率 $e = \dfrac{c}{a} = 2$. -
设 $ C $ 的右顶点为 $ A $,右焦点为 $ F $,$\left| {DF} \right|\cdot\left| {BF} \right| = 17$,证明:过 $ A $、$ B $、$ D $ 三点的圆与 $ x $ 轴相切.标注答案解析由 $ ①② $ 知,$ C $ 的方程为 $3{x^2} - {y^2} = 3{a^2}$,$A\left(a,0\right)$,$F\left(2a,0\right)$,${x_1} + {x_2} = 2$,${x_1}{x_2} = - \dfrac{{4 + 3{a^2}}}{2} < 0$,
故不妨设 ${x_1} \leqslant - a$,${x_2} \geqslant a$.
$\left| {BF} \right| = \sqrt {{{\left({x_1} - 2a\right)}^2} + y_1^2} = \sqrt {{{\left({x_1} - 2a\right)}^2} + 3x_1^2 - 3{a^2}} = a - 2{x_1}$,
$\left| {FD} \right| = \sqrt {{{\left({x_2} - 2a\right)}^2} + y_2^2} = \sqrt {{{\left({x_2} - 2a\right)}^2} + 3x_2^2 - 3{a^2}} = 2{x_2} - a$,
所以\[ \left| {BF} \right| \cdot \left| {FD} \right| = \left(a - 2{x_1}\right)\left(2{x_2} - a\right) = - 4{x_1}{x_2} + 2a\left({x_1} + {x_2}\right) - {a^2} = 5{a^2} + 4a + 8 .\]又 $\left| {BF} \right| \cdot \left| {FD} \right| = 17$,故 $5{a^2} + 4a + 8 = 17$,解得 $a = 1,$ 或 $a = - \dfrac{9}{5}$(舍去).
故\[ \left| {BD} \right| = \sqrt 2 \left| {{x_1} - {x_2}} \right| = \sqrt 2 \cdot \sqrt {{{\left({x_1} + {x_2}\right)}^2} - 4{x_1}{x_2}} = 6 .\]连接 $ MA $,则由 $A\left(1,0\right)$,$M\left(1,3\right)$ 知 $\left| {MA} \right| = 3$,从而 $MA = MB = MD$,且 $MA \bot x$ 轴,
因此以 $ M $ 为圆心,$ MA $ 为半径的圆经过 $ A $、$ B $、$ D $ 三点,且在点 $ A $ 处于 $x$ 轴相切.
所以过 $ A $、$ B $、$ D $ 三点的圆与 $x$ 轴相切.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2