如图，$ AB $ 是 $ ⊙O $ 的直径，$ D $ 为 $ ⊙O $ 上一点，过点 $ D $ 作 $ ⊙O $ 的切线交 $ AB $ 延长线于点 $ C $，若 $ DA=DC $，求证：$ AB=2BC $．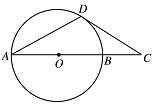
【难度】
【出处】
2010年高考江苏卷
【标注】
-
标注答案解析如图所示，连接 $ OD $，$ BD $，
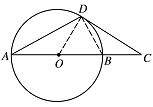因为 $ CD $ 为 $ ⊙O $ 的切线，$ AB $ 是直径，所以 $\angle ADB = \angle ODC =90^\circ$，
所以 $ \angle ODA= \angle BDC$．
又因为 $ DA=DC $，所以 $\angle DAB=\angle DCB$．
所以 $ \triangle ADO \cong \triangle CDB$．
所以 $OA=BC$，从而 $ AB=2BC $．
题目
问题1
答案1
解析1
备注1
