如图,$ A $、$ B $ 是海面上位于东西方向相距 $5\left( {3 + \sqrt 3 } \right)$ 海里的两个观测点,现位于 $ A $ 点北偏东 $ 45^\circ $,$ B $ 点北偏西 $ 60^\circ $ 的 $ D $ 点有一艘轮船发出求救信号,位于 $ B $ 点南偏西 $ 60^\circ $ 且与 $ B $ 点相距 $20\sqrt 3 $ 海里的 $ C $ 点的救援船立即前往营救,其航行速度为 $ 30 $ 海里 / 小时,该救援船到达 $ D $ 点需要多长时间?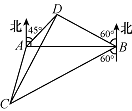

【难度】
【出处】
2010年高考陕西卷(理)
【标注】
-
标注答案解析由题意知\[AB = 5\left(3 + \sqrt 3 \right) ,\angle DBA = 90^\circ - 60^\circ = 30^\circ,\angle DAB = 45^\circ ,\]所以\[\angle ADB =180^\circ-\left(45^\circ+30^\circ\right) =105^\circ .\]在 $\triangle DAB$ 中,由正弦定理得\[\dfrac{DB}{\sin \angle DAB} = \dfrac{AB}{\sin \angle ADB},\]于是\[\begin{split}DB& = \dfrac{AB \cdot \sin \angle DAB}{\sin \angle ADB} = \dfrac{5\left(3 + \sqrt 3 \right) \cdot \sin 45^\circ }{\sin 105^\circ } \\&= \dfrac{5\left(3 + \sqrt 3 \right) \cdot \sin 45^\circ }{\sin 45^\circ \cdot \cos 60^\circ + \sin 60^\circ \cdot \cos 45^\circ }\\&=\dfrac{5\sqrt 3 \left(1 + \sqrt 3 \right)}{{\dfrac{\left(1 + \sqrt 3 \right)}{2}}} = 10\sqrt 3,\end{split}\]又\[\begin{split}\angle DBC &= \angle DBA + \angle ABC \\&= 30^\circ + \left(90^\circ - 60^\circ \right) = 60^\circ ,\end{split}\]在 $\triangle DBC$ 中,由余弦定理得\[\begin{split}C{D} &= \sqrt {B{D^2} + B{C^2} - 2BD \cdot BC \cdot \cos \angle DBC}\\&=\sqrt {300 + 1200 - 2 \times 10\sqrt 3 \times 20\sqrt 3 \times \dfrac{1}{2}}= 30,\end{split}\]则需要的时间为 $t = \dfrac{30}{30} = 1 $.
故救援船到达 $ D $ 点需要 $ 1 $ 小时.
题目
问题1
答案1
解析1
备注1