如图,已知椭圆 $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\left(a > b > 0\right)$ 的离心率为 $\dfrac{{\sqrt 2 }}{2}$,以该椭圆上的点和椭圆的左、右焦点 ${F_1},{F_2}$ 为顶点的三角形的周长为 $4\left(\sqrt 2 + 1\right)$,一等轴双曲线的顶点是该椭圆的焦点,设 $ P $ 为该双曲线上异于顶点的任一点,直线 $P{F_1}$ 和 $P{F_2}$ 与椭圆的交点分别为 $ A $、$ B $ 和 $ C $、$ D $.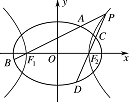

【难度】
【出处】
2010年高考山东卷(理)
【标注】
-
求椭圆和双曲线的标准方程;标注答案解析设椭圆的半焦距为 $c$,由题意知\[\dfrac{c}{a} = \dfrac{{\sqrt 2 }}{2},2a + 2c = 4\left(\sqrt 2 + 1\right),\]所以\[a = 2\sqrt 2 ,c = 2,\]又 ${a^2} = {b^2} + {c^2}$,因此 $b = 2$,故椭圆的标准方程为\[\dfrac{{{x^2}}}{8} + \dfrac{{{y^2}}}{4} = 1,\]由题意设等轴双曲线的标准方程为\[\dfrac{{{x^2}}}{{{m^2}}} - \dfrac{{{y^2}}}{{{m^2}}} = 1\left(m > 0\right),\]因为等轴双曲线的顶点是椭圆的焦点,所以\[m = 2,\]因此双曲线的标准方程为\[\dfrac{{{x^2}}}{4} - \dfrac{{{y^2}}}{4} = 1.\]
-
设直线 $P{F_1}$、$P{F_2}$ 的斜率分别为 ${k_1}$、${k_2}$,证明:${k_1} \cdot {k_2} = 1$;标注答案解析设 $A\left({x_1},{y_1}\right),B\left({x_2},{y_2}\right),P\left({x_0},{y_0}\right)$,则\[{k_1} = \dfrac{{{y_0}}}{{{x_0} + 2}},{k_2} = \dfrac{{{y_0}}}{{{x_0} - 2}},\]因为点 $ P $ 在双曲线 ${x^2} - {y^2} = 4$ 上,所以\[x_0^2 - y_0^2 = 4.\]因此\[\begin{split}{k_1}{k_2} &= \dfrac{{{y_0}}}{{{x_0} + 2}} \cdot \dfrac{{{y_0}}}{{{x_0} - 2}}\\& = \dfrac{{{y_0}}}{{x_0^2 - 4}} = 1,\end{split}\]即\[{k_1}{k_2} = 1.\]
-
是否存在常数 $\lambda $,使得 $\left| {AB} \right| + \left| {CD} \right| = \lambda \left| {AB} \right| \cdot \left| {CD} \right|$ 恒成立?若存在,求 $\lambda $ 的值;若不存在,请说明理由.标注答案解析由于 $ PF_{1} $ 的方程为 $y = {k_1}\left(x + 2\right)$,将其代入椭圆方程得\[\left(2k_1^2 + 1\right){x^2} - 8k_1^2x + 8k_1^2 - 8 = 0,\]由违达定理得\[{x_1} + {x_2} = \dfrac{{8k_1^2}}{{2k_1^2 + 1}},{x_1}{x_2} = \dfrac{{8k_1^2 - 8}}{{2k_1^2 + 1}},\]所以\[\begin{split}|AB| &= \sqrt {1 + k_1^2} \sqrt {{{\left({x_1} + {x_2}\right)}^2} - 4{x_1}{x_2}} \\& = \sqrt {1 + k_1^2} \sqrt {\left(\dfrac{{8k_1^2}}{{2k_1^2 - 1}}\right) - 4 \times \dfrac{{8k_1^2 - 8}}{{2k_1^2 + 1}}} \\&= 4\sqrt 2 \dfrac{{k_1^2 + 1}}{{2k_1^2 + 1}},\end{split}\]同理可得\[|CD| = 4\sqrt 2 \dfrac{{k_2^2 + 1}}{{2k_2^2 + 1}}.\]则\[\dfrac{1}{{|AB|}} + \dfrac{1}{{|CD|}} = \dfrac{1}{{4\sqrt 2 }}\left(\dfrac{{2k_1^2 + 1}}{{k_1^2 + 1}} + \dfrac{{2k_2^2 + 1}}{{k_2^2 + 1}}\right),\]又 ${k_1}{k_2} = 1$,所以\[\begin{split}\dfrac{1}{{|AB|}} + \dfrac{1}{{|CD|}} &= \dfrac{1}{{4\sqrt 2 }}\left(\dfrac{{2k_1^2 + 1}}{{k_1^2 + 1}} + \dfrac{{\dfrac{2}{{k_1^2}} + 1}}{{\dfrac{1}{{k_1^2}} + 1}}\right) \\&= \dfrac{{\sqrt 2 }}{8}\left(\dfrac{{2k_1^2 + 1}}{{k_1^2 + 1}} + \dfrac{{k_1^2 + 2}}{{k_1^2 + 1}}\right) \\&= \dfrac{{3\sqrt 2 }}{8},\end{split}\]故\[|AB| + |CD| = \dfrac{{3\sqrt 2 }}{8}|AB| \cdot |CD|,\]因此,存在 $\lambda = \dfrac{{3\sqrt 2 }}{8}$,使 $|AB| + |CD| = \lambda |AB| \cdot |CD|$ 恒成立.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3