如图,$ \triangle ABC $ 的角平分线 $ AD $ 的延长线交它的外接圆于点 $ E $.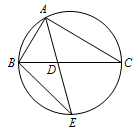

【难度】
【出处】
无
【标注】
-
证明:$ \triangle ABE \backsim \triangle ADC $;标注答案解析由已知条件,可得 $ \angle BAE=\angle CAD$.
因为 $ \angle AEB $ 与 $ \angle ACD $ 是同弧上的圆周角,所以\[ \angle AEB=\angle ACD. \]故\[ \triangle ABE \backsim \triangle ADC. \] -
若 $ \triangle ABC $ 的面积 $S=\dfrac{1}{2}AD\cdot AE$,求 $\angle BAC$ 的大小.标注答案解析因为 $ \triangle ABE \backsim \triangle ADC $,所以 $\dfrac{AB}{AE} = \dfrac{AD}{AC}$,即\[ AB \cdot AC=AD \cdot AE. \]又 $S=\dfrac{1}{2}AB \cdot AC\sin \angle BAC$,且 $S=\dfrac{1}{2}AD \cdot AE$,故\[ AB \cdot AC\sin \angle BAC=AD \cdot AE. \]则 $ \sin \angle BAC=1$.又 $ \angle BAC $ 为三角形内角,所以 $ \angle BAC=90^\circ $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2