如图,在 $ \triangle ABC $ 中,已知 $ \angle B=45^\circ $,$ D $ 是 $ BC $ 边上的一点,$ AD=10 $,$ AC=14 $,$ DC=6 $,求 $ AB $ 的长.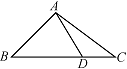

【难度】
【出处】
2010年高考陕西卷(文)
【标注】
-
标注答案解析在 $ \triangle ADC $ 中,$ AD=10 $,$ AC=14 $,$ DC=6 $,由余弦定理得\[ \cos \angle ADC =\dfrac{{A{D^2} + D{C^2} - A{C^2}}}{2AD\cdot DC}= \dfrac{100 + 36 - 196}{2 \times 10 \times 6} = - \dfrac{1}{2}, \]所以\[ \angle ADC=120^\circ , \angle ADB=60^\circ , \]在 $ \triangle ABD $ 中,$ AD=10 $,$\angle B=45^\circ $,$\angle ADB=60^\circ $,由正弦定理得\[\dfrac{AB}{\sin \angle ADB} = \dfrac{AD}{\sin B},\]所以\[ AB= \dfrac{AD\cdot\sin \angle ADB}{\sin B} = \dfrac{10\sin 60^\circ }{\sin 45^\circ } = \dfrac{{10 \times \dfrac{\sqrt 3 }{2}}}{{\dfrac{\sqrt 2 }{2}}} = 5\sqrt 6 .\]
题目
问题1
答案1
解析1
备注1