如图，在四棱锥 $ P-ABCD $ 中，底面 $ ABCD $ 是矩形，$ PA\perp 平面ABCD $，$ AP=AB $，$ BP=BC=2 $，$ E $、$ F $ 分别是 $ PB $、$ PC $ 的中点．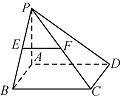
【难度】
【出处】
2010年高考陕西卷（文）
【标注】
-
证明：$ EF\parallel 平面PAD $；标注答案解析在 $ \triangle PBC $ 中，$ E $、$ F $ 分别是 $ PB $、$ PC $ 的中点，
所以 $ EF\parallel BC $．
因为 四边形 $ ABCD$ 为矩形，所以 $ BC\parallel AD $，
所以 $ EF\parallel AD $，
又 因为 $AD \subset 平面PAD$，$EF \not\subset 平面PAD $，
所以 $ EF\parallel 平面PAD $． -
求三棱锥 $ E-ABC $ 的体积 $ V $．标注答案解析连接 $ AE $，$ AC $，$ EC $，过 $ E $ 作 $ EG\parallel PA $ 交 $ AB $ 于点 $ G $，
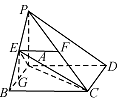则 $ EG\perp 平面ABCD $，且 $ EG= \dfrac{1}{2} PA $．
在 $ \triangle PAB $ 中，$ AP=AB $，$\angle PAB=90^\circ $，$ BP=2 $，所以\[AP=AB= \sqrt 2 ,EG=\dfrac{\sqrt 2 }{2}.\]所以\[ S_{\triangle ABC}=\dfrac{1}{2} AB\cdot BC= \dfrac{1}{2} \times \sqrt 2 \times 2= \sqrt 2 , \]所以\[ V_{E-ABC}= \dfrac{1}{3} S_{\triangle ABC}\cdot EG= \dfrac{1}{3} \times \sqrt 2 \times \dfrac{\sqrt 2 }{2}= \dfrac{1}{3} .\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
