如图,在四面体 $ ABOC $ 中,$ OC\perp OA $,$ OC\perp OB $,$ \angle AOB=120^\circ $,且 $ OA=OB=OC=1 $.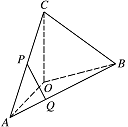

【难度】
【出处】
2010年高考湖北卷(文)
【标注】
-
设 $ P $ 为 $ AC $ 的中点,$ Q $ 在 $ AB $ 上且 $ AB=3AQ $,证明:$ PQ\perp OA $;标注答案解析解法一:如图,在平面 $ OAB $ 内作 $ ON \perp OA $ 交 $ AB $ 于 $ N $,连接 $ CN $.
 在 $ \triangle AOB $ 中,$\because $ $\angle AOB = {120^ \circ }$ 且 $ OA=OB $,
在 $ \triangle AOB $ 中,$\because $ $\angle AOB = {120^ \circ }$ 且 $ OA=OB $,
$\therefore$ $\angle OAB=\angle OBA=30^\circ$.
在 ${\mathrm{Rt}}\triangle AON $ 中,$\because$ $ \angle OAN=30^\circ$,$ \therefore $ $ ON = \dfrac{1}{2}AN$.
在 $ \triangle ONB $ 中,$\because$ $ \angle NOB=120^\circ-90^\circ=30^\circ=\angle OBN$,
$ \therefore $ $NB = ON = \dfrac{1}{2}AN$.
又 $ AB=3AQ $,$\therefore $ $ Q $ 为 $ AN $ 的中点.
在 $ \triangle CAN $ 中,$\because $ $P,Q$ 分别为 $ AC $,$ AN $ 的中点,$\therefore$ $ PQ\parallel CN$.
由 $ OA \perp OC $,$ OA \perp ON $ 知:$ OA \perp 平面CON $.
又 $ NC \subset 平面CON $,$\therefore $ $ OA\perp CN $.
由 $ PQ\parallel CN $,知 $ OA \perp PQ $.
解法二:取 $ O $ 为坐标原点,以 $ OA $,$ OC $ 所在的直线为 $ x $ 轴,$ z $ 轴,建立空间直角坐标系 $ O-xyz $(如图所示).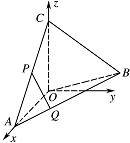 则 $A\left(1,0,0\right)$,$C\left(0,0,1\right)$,$B \left( - \dfrac{1}{2},\dfrac{{\sqrt 3 }}{2},0\right) $.
则 $A\left(1,0,0\right)$,$C\left(0,0,1\right)$,$B \left( - \dfrac{1}{2},\dfrac{{\sqrt 3 }}{2},0\right) $.
$\because$ $P$ 为 $AC$ 中点,$\therefore$ $P\left(\dfrac{1}{2},0,\dfrac{1}{2}\right)$.$\because$ $ \overrightarrow {AB} = \left( - \dfrac{3}{2},\dfrac{{\sqrt 3 }}{2},0\right)$.
又由已知,可得\[\overrightarrow {AQ} = \dfrac{1}{3}\overrightarrow {AB} = \left( - \dfrac{1}{2},\dfrac{{\sqrt 3 }}{6},0\right).\]又\[\overrightarrow {OQ}=\overrightarrow {OA} +\overrightarrow {AQ} =\left(\dfrac{1}{2},\dfrac{{\sqrt {3} }}{6},0\right).\]所以\[ \overrightarrow {PQ} =\overrightarrow {OQ} -\overrightarrow {OP}= \left(0,\dfrac{{\sqrt{3} }}{6}, - \dfrac{1}{2}\right),\]所以\[ \overrightarrow {PQ} \cdot\overrightarrow {OA} =\left(0,\dfrac{{\sqrt {3} }}{6}, - \dfrac{1}{2}\right)\cdot\left(1,0,0\right) = 0.\]故 $\overrightarrow {PQ} \perp \overrightarrow {OA} $. -
求二面角 $ O-AC-B $ 的平面角的余弦值.标注答案解析解法一:如图,连结 $ PN $,$ PO $.
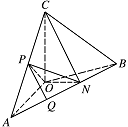 由 $ OC \perp OA $,$ OC \perp OB $ 知:$ OC \perp 平面OAB $.
由 $ OC \perp OA $,$ OC \perp OB $ 知:$ OC \perp 平面OAB $.
又 $ ON \subset 平面OAB $,$\therefore $ $ OC \perp ON $.
又由 $ ON \perp OA $ 知:$ ON \perp 平面AOC $.
$\therefore $ $ OP $ 是 $ NP $ 在平面 $ AOC $ 内的射影.
在等腰 $ {\mathrm{Rt}}\triangle COA $ 中,$ P $ 为 $ AC $ 的中点,$\therefore $ $ AC \perp OP $.
根据三垂线定理,知:$ AC \perp NP $.
$\therefore $ $\angle OPN$ 为二面角 $ O-AC-B $ 的平面角.
在等腰 $ {\mathrm{Rt}}\triangle COA $ 中,$ OC=OA=1 $,$\therefore $ $OP= \dfrac{{\sqrt 2 }}{2}$.
在 $ {\mathrm{Rt}}\triangle AON $ 中,$ON=OA \tan {30^ \circ } =\dfrac{{\sqrt 3 }}{3}$,
$\therefore $ 在 $ {\mathrm{Rt}}\triangle PON $ 中,$PN= \dfrac{{\sqrt {30} }}{6}$,所以\[\cos \angle OPN = \dfrac{{OP}}{{PN}} = \dfrac{{\dfrac{{\sqrt 2 }}{2}}}{{\dfrac{{\sqrt {30} }}{6}}} = \dfrac{{\sqrt {15} }}{5}.\]解法二:记平面 $ ABC $ 的法向量 $\overrightarrow n = \left(\overrightarrow n_1,{\overrightarrow n_2},{\overrightarrow n_3}\right)$,
则由 $\overrightarrow n \perp \overrightarrow {CA} $,$\overrightarrow n \perp \overrightarrow {AB} $,且 $\overrightarrow {CA} =\left(1,0,-1\right)$.得\[{\begin{cases}
{n_1} - {n_3} = 0, \\
- \dfrac{3}{2}{n_2} + \dfrac{{\sqrt 3 }}{2}{n_2} = 0, \\
\end{cases}}\]故可取 $\overrightarrow n = \left(1,\sqrt 3 ,1\right)$,又平面 $ OAC $ 的法向量为 $ \overrightarrow e=\left(0,1,0\right) $.所以\[\cos \left \langle\overrightarrow n,\overrightarrow e \right \rangle= \dfrac{{\left(1,\sqrt 3 ,1\right)\cdot\left(0,1,0\right)}}{{\sqrt 5 \times1}} = \dfrac{{\sqrt 3 }}{{\sqrt 5 }},\]二面角 $ O-AC-B $ 的平面角是锐角,记为 $\theta $,则 $\cos \theta = \dfrac{{\sqrt {15} }}{5}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2