某营养师要为某个儿童预定午餐和晚餐．已知一个单位的午餐含 $ 12 $ 个单位的碳水化合物，$ 6 $ 个单位的蛋白质和 $ 6 $ 个单位的维生素 ${\mathrm{C}}$；一个单位的晚餐含 $ 8 $ 个单位的碳水化合物，$ 6 $ 个单位的蛋白质和 $ 10 $ 个单位的维生素 ${\mathrm{C}}$．另外，该儿童这两餐需要的营养中至少含 $ 64 $ 个单位的碳水化合物，$ 42 $ 个单位的蛋白质和 $ 54 $ 个单位的维生素 ${\mathrm{C}}$．如果一个单位的午餐、晚餐的费用分别是 $ 2.5 $ 元和 $ 4 $ 元，那么要满足上述的营养要求，并且花费最少，应当为该儿童分别预订多少个单位的午餐和晚餐？
【难度】
【出处】
2010年高考广东卷（理）
【标注】
-
标注答案解析设为该儿童分别预订 $x、y$ 个单位的午餐和晚餐，共花费 $z$ 元，则 $z = 2.5x + 4y$，
且满足以下条件\[{\begin{cases}
12x + 8y \geqslant 64, \\
6x + 6y \geqslant 42 ,\\
6x + 10y \geqslant 54, \\
x,y \geqslant 0, \\
\end{cases}}\]化简得\[{\begin{cases}3x + 2y \geqslant 16, \\
x + y \geqslant 7, \\
3x + 5y \geqslant 27 ,\\
x,y \geqslant 0 ,\\
\end{cases}}\]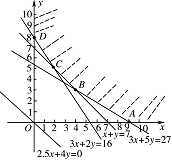
作出可行域如图，则 $z $ 在可行域的四个顶点 $ A\left(9,0\right)$，$B\left(4,3\right) $，$C\left(2,5\right) $，$ D\left(0,8\right)$ 处的值分别为\[ \begin{split}z_A&=2.5\times9+4\times0=22.5,\\z_B&=2.5\times4+4\times3=22,\\z_C&=2.5\times2+4\times5=25,\\z_D&=2.5\times0+4\times8=32.\end{split}\]比较之，$ z_B$ 最小，因此应当为该儿童预定 $ 4 $ 个单位的午餐和 $ 3 $ 个单位的晚餐，就可以满足要求．
题目
问题1
答案1
解析1
备注1
