如图,已知圆上的弧 $\overparen {AC} = \overparen {BD}$,过 $ C $ 点的圆的切线与 $ BA $ 的延长线交于 $ E $ 点,证明: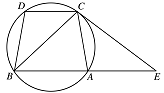

【难度】
【出处】
2010年高考新课标全国卷(文)
【标注】
-
$\angle ACE = \angle BCD$;标注答案解析因为 $\overparen {AC} = \overparen {BD}$,所以 $\angle BCD = \angle ABC$.
又因为 $EC$ 与圆相切于点 $C$,故 $\angle ACE = \angle ABC$,
所以 $\angle ACE = \angle BCD$. -
$B{C^2} =BE \times CD$.标注答案解析因为 $\angle ECB = \angle CDB$,$\angle EBC = \angle BCD$,
所以 $\triangle BDC \backsim \triangle ECB$,故 $\dfrac{{BC}}{{BE}} = \dfrac{{CD}}{{BC}}$.
即 $B{C^2} = BE \times CD$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2