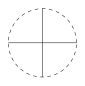
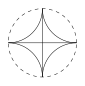
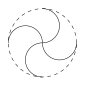
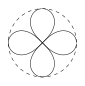
如图,一个直径为 $ 1 $ 的小圆沿着直径为 $ 2 $ 的大圆内壁逆时针方向滚动,$M$ 和 $N$ 是小圆的一条固定直径的两个端点.那么,当小圆这样滚过大圆内壁一周,点 $M,N$ 在大圆内所绘出的图形大致是 \((\qquad)\) 

【难度】
【出处】
2011年高考江西卷(理)
【标注】
【答案】
A
【解析】
根据小圆半径与大圆半径 $1:2$ 的关系,找上下左右四个点,根据这四个点的位置,小圆转半圈,刚好是大圆的四分之一,因此 $M$ 点的轨迹和 $N$ 点的轨迹是四条线段,刚好是的大圆的半径.
也可以根据某一个位置进行分析,在小圆上取一点 $A$,当点 $A$ 转到大圆内壁上时(即点 $A_1$),小圆圆心转到 $O_1$ 点,此时要找到点 $M$ 与点 $N$ 的新位置,因为在小圆上,$M,A,N$ 三点的相对位置不变,即 $\angle MOA$ 大小不变;又在小圆上 $\overparen {AM}$ 的长等于大圆上 $\overparen {A_1M}$ 的长,故点 $O_1,A_1,N$ 共线.所以四边形 $A_1N_1NM_1$ 为矩形,故点 $M_1$ 在线段 $MN$ 上,如图:
也可以根据某一个位置进行分析,在小圆上取一点 $A$,当点 $A$ 转到大圆内壁上时(即点 $A_1$),小圆圆心转到 $O_1$ 点,此时要找到点 $M$ 与点 $N$ 的新位置,因为在小圆上,$M,A,N$ 三点的相对位置不变,即 $\angle MOA$ 大小不变;又在小圆上 $\overparen {AM}$ 的长等于大圆上 $\overparen {A_1M}$ 的长,故点 $O_1,A_1,N$ 共线.所以四边形 $A_1N_1NM_1$ 为矩形,故点 $M_1$ 在线段 $MN$ 上,如图:

题目
答案
解析
备注