如图，对于任一给定的四面体 ${A_1}{A_2}{A_3}{A_4}$，找出依次排列的四个相互平行的平面 ${\alpha _1}, {\alpha _2} , {\alpha _3} , {\alpha _4}$，使得 ${A_i} \in {\alpha _i} \left( {i = 1,2,3,4} \right)$，且其中每相邻两个平面间的距离都相等；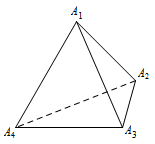
【难度】
【出处】
无
【标注】
【答案】
【解析】
如图所示，取 ${A_1}{A_4}$ 的三等分点 ${P_2} , {P_3}$，${A_1}{A_3}$ 的中点 $M$，${A_2}{A_4}$ 的中点 $N$．
过三点 ${A_2},{P_2},M$ 作平面 ${\alpha _2}$，过三点 ${A_3},{P_3},N$ 作平面 ${\alpha _3}$，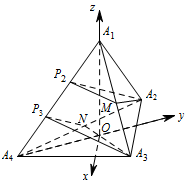
因为 ${A_2}{P_2}\parallel N{P_3}$，${A_3}{P_3}\parallel M{P_2}$，所以平面 ${\alpha _2}$ $\parallel $ 平面 ${\alpha _3}$，
再过点 ${A_1},{A_4}$ 分别作平面 ${\alpha _1},{\alpha _4}$ 与平面 ${\alpha _2}$ 平行，那么四个平面 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ 依次相互平行，
由线段 ${A_1}{A_4}$ 被平行平面 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ 截得的线段相等知，其中每相邻两个平面间的距离相等，故 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ 为所求平面．
过三点 ${A_2},{P_2},M$ 作平面 ${\alpha _2}$，过三点 ${A_3},{P_3},N$ 作平面 ${\alpha _3}$，
因为 ${A_2}{P_2}\parallel N{P_3}$，${A_3}{P_3}\parallel M{P_2}$，所以平面 ${\alpha _2}$ $\parallel $ 平面 ${\alpha _3}$，再过点 ${A_1},{A_4}$ 分别作平面 ${\alpha _1},{\alpha _4}$ 与平面 ${\alpha _2}$ 平行，那么四个平面 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ 依次相互平行，
由线段 ${A_1}{A_4}$ 被平行平面 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ 截得的线段相等知，其中每相邻两个平面间的距离相等，故 ${\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}$ 为所求平面．
答案
解析
备注
