底面边长为 $ 2 $ 的正三棱锥 $P - ABC$,其表面展开图是三角形 ${P_1}{P_2}{P_3}$,如图.求 $\triangle {P_1}{P_2}{P_3}$ 的各边长及此三棱锥的体积 $V$.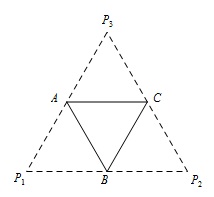

【难度】
【出处】
无
【标注】
-
标注答案解析由题知,三棱锥 $P - ABC$ 是正三棱锥,
所以 侧棱与底边所成角相同且底面 $\triangle ABC$ 是边长为 $ 2 $ 的正三角形,
由题得,$\angle ABC = \angle BCA = \angle CAB = \dfrac{\pi }{3}$,\[\angle {P_1}BA = \angle {P_1}AB = \angle {P_2}BC = \angle {P_2}CB = \angle {P_3}AC = \angle {P_3}CA,\]又 $A,B,C$ 三点恰好在 ${P_1},{P_2},{P_3}$ 构成的 $\triangle {P_1}{P_2}{P_3}$ 的三条边上,
所以\[\begin{split}\angle {P_1}BA & = \angle {P_1}AB \\& = \angle {P_2}BC = \angle {P_2}CB \\& = \angle {P_3}AC = \angle {P_3}CA \\& = \dfrac{\pi }{3},\end{split}\]所以\[\begin{split}{P_1}A & = {P_1}B \\& = {P_2}B = {P_2}C \\& = {P_3}C = {P_3}A \\& = 2,\end{split}\]故\[{P_1}{P_2} = {P_1}{P_3} = {P_2}{P_3} = 4,\]三棱锥 $P - ABC$ 是边长为 $ 2 $ 的正四面体,
设顶点 $P$ 在底面 $ABC$ 内的投影为 $O$,连接 $BO$,并延长交 $AC$ 于 $D$,
所以 $D$ 为 $AC$ 中点,$O$ 为 $\triangle ABC$ 的重心,$PO \perp $ 底面 $ABC$,
可得出\[\begin{split}BO & = \dfrac{2}{3}BD = \dfrac{{2\sqrt 3 }}{3}, \\ PO & = \dfrac{{2\sqrt 6 }}{3},\end{split}\]因此\[\begin{split}V & = \dfrac{1}{3} \cdot \dfrac{1}{2} \cdot 2 \cdot 2 \cdot \dfrac{{\sqrt 3 }}{2} \cdot \dfrac{{2\sqrt 6 }}{3} \\& = \dfrac{{2\sqrt 2 }}{3}.\end{split}\]
题目
问题1
答案1
解析1
备注1