如图,在正方形 $ABCD$ 中,$E,G$ 分别在边 $DA,DC$ 上(不与端点重合),且 $DE=DG$,过点 $D$ 作 $DF\perp CE$,垂足为 $F$.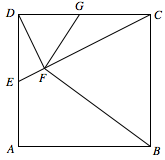

【难度】
【出处】
无
【标注】
-
证明:$B,C,G,F$ 四点共圆;标注答案略解析只要证明四边形 $BCGF$ 有一组对角互补即可.因为 $DF\perp CE$,
所以 $ \mathrm {Rt} \triangle DEF\backsim \mathrm {Rt} \triangle CED$,
所以 $\angle GDF=\angle DEF=\angle BCF$,$\dfrac{DF}{DE}=\dfrac{CF}{CD}$.
因为 $DE=DG$,$CD=BC$,
所以 $\dfrac{DF}{DG}=\dfrac{CF}{BC}$,
所以 $\triangle GDF\backsim \triangle BCF$,
所以 $\angle CFB=\angle DFG$,
所以 $\angle GFB=\angle GFC+\angle CFB=\angle GFC+\angle DFG=\angle DFC=90^\circ$,
所以 $\angle GFB+\angle GCB=180^\circ $.
所以 $B,C,G,F$ 四点共圆. -
若 $AB=1,E$ 为 $DA$ 的中点,求四边形 $BCGF$ 的面积.标注答案$ \dfrac{1}{2}$解析由第(1)小题的结论,将四边形 $BCGF$ 放在圆中进行思考.因为 $E$ 为 $AD$ 中点,$AB=1$,
所以 $DG=CG=DE=\dfrac{1}{2}$,
所以在 $ \mathrm {Rt} \triangle DFC$ 中,$GF=GC$,
连接 $GB$,$ \mathrm {Rt} \triangle BCG\cong \mathrm {Rt} \triangle BFG$,
所以\[{{S}_{BCGF}}=2{{S}_{\triangle BCG}} = 2\times \dfrac{1}{2}\times 1\times \dfrac{1}{2} = \dfrac{1}{2}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2