（i）\[ f ′\left(x\right)=12ax^2-2b=12a \left(x^2-{\dfrac{b}{6a}}\right) . \]当 $ b\leqslant 0 $ 时，有\[ f ′\left(x\right)\geqslant 0 ,\]此时 $ f\left(x\right) $ 在 $ \left[0,+\infty \right) $ 上单调递增．
当 $ b>0 $ 时，\[ f ′\left(x\right)=12a\left( x+{\sqrt{{\dfrac{b}{6a}}}}\right)\left( x-{\sqrt{{\dfrac{b}{6a}}}}\right) , \]此时 $ f\left(x\right) $ 在 $\left[ 0,{\sqrt{{\dfrac{b}{6a}}}} \right] $ 上单调递减，在 $\left[ {\sqrt{{\dfrac{b}{6a}}}},+\infty \right) $ 上单调递增．
所以当 $ 0\leqslant x\leqslant 1 $ 时，\[ \begin{split}f\left(x\right)_{{\mathrm{max}}} &=\max\limits \left\{f\left(0\right),f\left(1\right)\right\}\\&=\max\limits \left\{-a+b,3a-b\right\}\\&= \begin{cases}3a-b,b\leqslant 2a,\\-a+b,b>2a ,\end{cases}\\&=|2a-b|+a.\end{split}\]（ii）由于 $ 0\leqslant x\leqslant 1 $，故当 $ b\leqslant 2a $ 时，\[ \begin{split}f\left(x\right)+|2a-b|+a &=f\left(x\right)+3a-b\\&=4ax^3-2bx+2a\\&\geqslant 4ax^3-4ax+2a\\&=2a\left(2x^3-2x+1\right). \end{split}\]当 $ b>2a $ 时，\[ \begin{split}f\left(x\right)+|2a-b|+a &=f\left(x\right)-a+b\\&=4ax^3+2b\left(1-x\right)-2a\\&>4ax^3+4a\left(1-x\right)-2a\\&=2a\left(2x^3-2x+1\right).\end{split} \]设 $ g\left(x\right)=2x^3-2x+1,0\leqslant x\leqslant 1 $，则\[ g′\left(x\right)=6x^2-2=6 \left(x-{\dfrac{{\sqrt{3}}}{3}}\right)\left( x+{\dfrac{{\sqrt{3}}}{3}}\right) , \]于是 $g'\left(x\right),g\left(x\right)$ 随 $x$ 的变化情况如下表：\begin{array}{|c|c|c|c|c|c|} \hline
x& 0 &\left(0,{\dfrac{{\sqrt{3}}}{3}} \right)&{\dfrac{{\sqrt{3}}}{3}} &\left({\dfrac{{\sqrt{3}}}{3}},1\right) &1\\ \hline
g ′\left(x\right) &&-& 0 &+&\\ \hline
g\left(x\right) &1 &减& 极小值 &增 &1\\ \hline\end{array}所以，\[ g\left(x\right)_{{\mathrm{min}}}=g \left({\dfrac{{\sqrt{3}}}{3}} \right)=1-{\dfrac{4{\sqrt{3}}}{9}}>0. \]所以当 $ 0\leqslant x\leqslant 1 $ 时，\[ 2x^3-2x+1>0. \]从而\[ f\left(x\right)+|2a-b|+a\geqslant 2a\left(2x^3-2x+1\right)\geqslant 0. \]

由（i）知，当 $ 0\leqslant x\leqslant 1 $，\[ f\left(x\right)_{{\mathrm{max}}}=|2a-b|+a, \]所以\[ |2a-b|+a\leqslant 1. \]若 $ |2a-b|+a\leqslant 1 $，则由（ii）的结论知\[ f\left(x\right)\geqslant -\left(|2a-b|+a\right)\geqslant -1. \]所以 $ -1\leqslant f\left(x\right)\leqslant 1 $ 对任意 $ 0\leqslant x\leqslant 1 $ 恒成立的充要条件是\[ \begin{cases}|2a-b|+a\leqslant 1,\\a>0,\end{cases} \]即\[ \begin{cases}2a-b\geqslant 0,\\3a-b\leqslant 1,\\a>0, \end{cases}或 \begin{cases}2a-b<0,\\b-a\leqslant 1,\\a>0.\end{cases} \quad \cdots \cdots ① \]在直角坐标系 $ aOb $ 中，$ ① $ 所表示的平面区域为如图所示的阴影部分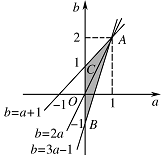，其中不包括线段 $ BC $．作一组平行直线 $ a+b=t\left(t\in {\mathbb{R}}\right) $，得\[ -1<a+b\leqslant 3,\]所以 $ a+b $ 的取值范围是 $ \left(-1,3\right] $．