查看数据源：599165c22bfec200011e03df
某几何体的三视图如图所示，则该几何体的表面积等于 \((\qquad)\)
A: $8+2\sqrt 2$
B: $11+2\sqrt 2$
C: $14+2\sqrt 2$
D: $15$
【难度】
【出处】
2015年高考福建卷（文）
【标注】
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的三视图
  • 知识点
    >
    立体几何
    >
    空间几何体
    >
    空间几何体的形体分析
    >
    空间几何体的表面积
【答案】
B
【解析】
根据三视图确定出原图形为直四棱柱，再结合三视图上的长度，确定出原图形的各棱长，进而求出表面积．由三视图知，该几何体是一个直四棱柱，上下底面为直角梯形，如图所示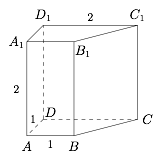．直角梯形斜腰长为 $BC=\sqrt2$，因此底面周长为 $4+\sqrt2$，侧面积为\[2\cdot\left(4+\sqrt2\right)=8+2\sqrt2,\]两个底面的面积和为 $3$，因此该几何体的表面积为 $11+2\sqrt2$．
题目 答案 解析 备注
0.118995s