已知抛物线 ${C_1}:{x^2} = y$,圆 ${C_2}:{x^2} + {\left(y - 4\right)^2} = 1$ 的圆心为点 $M$.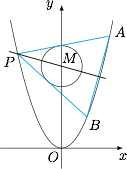

【难度】
【出处】
2011年高考浙江卷(理)
【标注】
-
求点 $M$ 到抛物线 ${C_1}$ 的准线的距离;标注答案略解析由题意可知,抛物线的准线方程为:\[y = - \dfrac{1}{4},\]所以圆心 $M\left( {0,4} \right)$ 到准线的距离是 $\dfrac{17}{4}$.
-
已知点 $P$ 是抛物线 ${C_1}$ 上一点(异于原点),过点 $P$ 作圆 ${C_2}$ 的两条切线,交抛物线 ${C_1}$ 于 $A$,$B$ 两点,若过 $M$,$P$ 两点的直线 $l$ 垂直于 $AB$,求直线 $l$ 的方程.标注答案略解析设 $P\left( {{x_0},x_0^2} \right)$,$A\left( {{x_1},x_1^2} \right)$,$B\left( {{x_2},x_2^2} \right)$,由题意得\[{x_0}\ne 0,{x_0} \ne \pm 1 , {x_1} \ne {x_2}.\]设过点 $P$ 的圆 ${C_2}$ 的切线方程为\[y - {x_0^2} = k\left(x - {x_0}\right), \]即\[y=kx-kx_0+{x_0}^2 \quad \cdots \cdots ① \]则\[\dfrac{{ \left|k{x_0} + 4 - x_0^2 \right|}}{{\sqrt {1 + {k^2}} }} = 1,\]即\[\left(x_0^2 - 1\right){k^2} + 2{x_0}\left(4 - x_0^2\right)k + {\left(x_0^2 - 4\right)^2} - 1 = 0,\]设 $PA$,$PB$ 的斜率为 ${k_1}$,${k_2}\left({k_1} \ne {k_2}\right)$,则 ${k_1}$,${k_2}$ 是上述方程的两根,所以\[\begin{split}{k_1} + {k_2} & = \dfrac{{2{x_0}\left({x_0^2} - 4\right)}}{{{x_0^2} - 1}} , \\ {k_1} \cdot {k_2} & = \dfrac{{{{\left({x_0^2} - 4\right)}^2} - 1}}{{{x_0^2} - 1}},\end{split}\]将 ① 代入 $y = {x^2}$ 得\[{x^2} - kx + k{x_0} - {x_0^2} = 0,\]由于 ${x_0}$ 是此方程的根,故\[{x_1} = {k_1} - {x_0} \]同理有\[ {x_2} = {k_2} - {x_0}\]所以\[\begin{split}{k_{AB}} & = \dfrac{{{x_1^2} - {x_2^2}}}{{{x_1} - {x_2}}} = {x_1} + {x_2} = {k_1} + {k_2} - 2{x_0} \\& = \left( {\dfrac{{2{x_0}\left( {x_0^2 - 4} \right)}}{{{x_0^2} - 1}}} \right) - 2{x_0} , \\ {k_{MP}} & = \dfrac{{{x_0^2} - 4}}{x_0}.\end{split}\]由 $MP \perp AB$,得\[{k_{AB}} \cdot {k_{MP}} = \left[ {\dfrac{{2{x_0}\left( {x_0^2 - 4} \right)}}{{{x_0^2} - 1}} - 2{x_0}} \right] \cdot {\dfrac{x_0^2 - 4}{x_0}} = - 1,\]解得\[ {x_0^2} = \dfrac{23}{5} ,\]即点 $P$ 的坐标为 $\left( { \pm \sqrt {\dfrac{23}{5}} ,\dfrac{23}{5}} \right)$,所以直线 $l$ 的方程为\[y = \pm \dfrac{{3\sqrt {115} }}{115}x + 4.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2