如图,$D,E,F$ 分别是 $\triangle{ABC}$ 的边 $BC,CA,AB$ 上的点,且 $DE\cap AB=F_0$,$EF\cap BC=D_0$,$FD\cap CA=E_0$.证明:$AD,BE,CF$ 三线共点,当且仅当 $D_0,E_0,F_0$ 三点共线.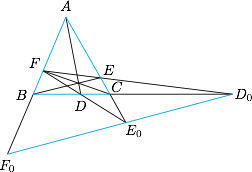

【难度】
【出处】
2011年全国高中数学联赛山西省预赛
【标注】
【答案】
略
【解析】
据梅涅劳斯定理,$D_0,E_0,F_0$ 三点共线,当且仅当$$\dfrac{AE_0}{E_0C}\cdot \dfrac{CD_0}{D_0B}\cdot \dfrac{BF_0}{F_0A}=1.$$而据塞瓦定理,$AD,BE,CF$ 三线共点,当且仅当$$\dfrac{BD}{DC}\cdot \dfrac{CE}{EA}\cdot \dfrac{AF}{FB}=1.$$因直线 $D_0EF$ 截 $\triangle{ABC}$,得到$$\dfrac{CE}{EA}\cdot \dfrac{AF}{FB}\cdot \dfrac{BD_0}{D_0C}=1,$$所以$$\dfrac{CD_0}{D_0B}=\dfrac{CE}{EA}\cdot \dfrac{AF}{FB}.$$同理,由直线 $E_0DF$ 截 $\triangle{ABC}$ 得$$\dfrac{CE_0}{E_0A}=\dfrac{CD}{DB}\cdot \dfrac{BF}{FA},$$由直线 $F_0DE$ 截 $\triangle{ABC}$ 得$$\dfrac{BF_0}{F_0A}=\dfrac{BD}{DC}\cdot \dfrac{CE}{EA},$$因此,$$\dfrac{AE_0}{E_0C}\cdot \dfrac{CD_0}{D_0B}\cdot \dfrac{BF_0}{F_0A}=\left(\dfrac{BD}{DC}\cdot \dfrac{CE}{EA}\cdot \dfrac{AF}{FB}\right)^2,$$由于该等式中的一端取值为 $1$ 当且仅当其另一端也取值为 $1$,故结论得证.
答案
解析
备注