如图,$P$ 是抛物线 $y^2=2x$ 上的动点,点 $B,C$ 在 $y$ 轴上,圆 $(x-1)^2+y^2=1$ 内切于 $\triangle PBC$,求 $\triangle PBC$ 面积的最小值.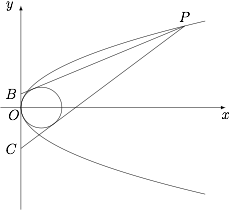

【难度】
【出处】
2008年全国高中数学联赛(一试)
【标注】
【答案】
$8$
【解析】
由抛物线的对称性,设 $P\left(2t^2,2t\right)$,其中 $t>1$.点 $P$ 对圆的双切线方程为\[\left[(x-1)^2+y^2-1\right]\cdot \left[(2t^2-1)^2+(2t)^2-1\right]-\left[(x-1)\cdot \left(2t^2-1\right)+y\cdot 2t-1\right]^2=0.\]令 $x=0$,可得\[4t^2\left[\left(t^2-1\right)y^2+2ty-t^2\right]=0,\]于是 $B\left(0,\dfrac{t}{1+t}\right)$,$C\left(0,\dfrac{t}{1-t}\right)$.进而 $\triangle PBC$ 的面积\[\begin{split}S&=\dfrac 12\cdot \left|\dfrac{t}{1+t}-\dfrac{t}{1-t}\right|\cdot 2t^2\\
&=\dfrac{2t^4}{t^2-1}\\
&=2\left[2+(t^2-1)+\dfrac{1}{t^2-1}\right]\\
&\geqslant 8,\end{split}\]等号当 $t=\sqrt 2$ 时取得.因此所求面积的最小值为 $8$.
&=\dfrac{2t^4}{t^2-1}\\
&=2\left[2+(t^2-1)+\dfrac{1}{t^2-1}\right]\\
&\geqslant 8,\end{split}\]等号当 $t=\sqrt 2$ 时取得.因此所求面积的最小值为 $8$.
答案
解析
备注