在 $\mathrm {Rt}\triangle ABC$ 中，$\angle BAC=90^\circ$，$AC=AB=4$，$D,E$ 分别是 $AB,AC$ 的中点．若等腰 $\mathrm {Rt}\triangle ADE$ 绕点 $A$ 旋转，得到等腰 $\mathrm {Rt}\triangle AD_1E_1$，记直线 $BD_1$ 与 $CE_1$ 的交点为 $P$．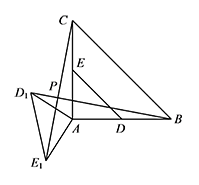
【难度】
【出处】
无
【标注】
-
设 $BC$ 的中点为 $M$，求线段 $PM$ 的长；标注答案$PM=\dfrac 12BC=2\sqrt 2$解析易证 $\triangle E_1AC\cong \triangle D_1AB$，
所以 $\angle E_1CA=\angle D_1BA$．
从而 $A,B,C,P$ 四点共圆，
所以 $\angle BPC=\angle BAC=90^\circ$．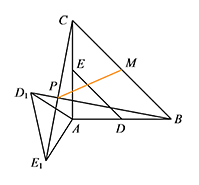
如图，因为点 $M$ 是 $\mathrm{Rt}\triangle BPC$ 斜边的中点，
所以 $PM=\dfrac 12BC=2\sqrt 2$． -
求点 $P$ 到 $AB$ 所在直线的距离的最大值．标注答案$1+\sqrt 3$解析由题意知，点 $D_1,E_1$ 在以 $A$ 为圆心、$AD$ 为半径的圆上，而点 $P$ 在直线 $BD_1$ 上，所以当直线 $BD_1$ 与 $\odot A$ 相切时，点 $P$ 到直线 $AB$ 的距离最大．此时四边形 $AD_1PE_1$ 是正方形，即 $PD_1=AD_1=2$．
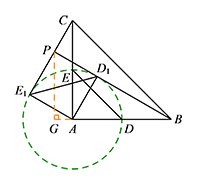如图所示，作 $PG\perp AB$ 于点 $G$，则在 $\mathrm{Rt}\triangle AD_1B$ 中，
有 $\angle ABD_1=30^\circ, BD_1=2\sqrt 3$．
所以 $PG=\dfrac 12PB=1+\sqrt 3$，
即点 $P$ 到 $AB$ 所在直线的距离的最大值为 $1+\sqrt 3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
