在 $\triangle ABC$ 中，$\angle ABC=90^\circ$，$D$ 为平面内一动点，$AD=a$，$AC=b$，其中 $a,b$ 为常数，且 $a<b$．将 $\triangle ABD$ 沿射线 $BC$ 方向平移，得到 $\triangle FCE$，点 $A,B,D$ 的对应点分别为 $F,C,E$，连接 $BE$．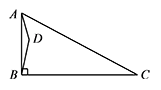
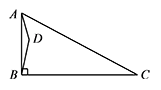
【难度】
【出处】
无
【标注】
-
如图，若点 $D$ 在 $\triangle ABC$ 的内部，请在图中画出 $\triangle FCE$；标注答案如图：
解析略 -
在 $(1)$ 的条件下，若 $AD\perp BE$，求 $BE$ 的长（用含 $a,b$ 的式子表示）；标注答案$BE=\sqrt{b^2-a^2}$解析连接 $BF$．
由平移的基本性质，易证四边形 $ABCF$ 为矩形，四边形 $ADEF$ 是平行四边形．
因为 $AD\perp BE$，所以 $FE\perp BE, BF=AC=b$．
在 $\mathrm{Rt}\triangle BEF$ 中，由勾股定理得 $BE=\sqrt{b^2-a^2}$． -
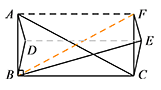
若 $\angle BAC=\alpha$，求当线段 $BE$ 的长度最大和最小时，$\angle BAD$ 的大小（用含 $\alpha$ 的式子表示）．标注答案① 线段 $BE$ 的长度最大时，$\angle BAD=\angle CFE=180^\circ-\alpha$；
② 线段 $BE$ 的长度最小时，$\angle BAD=\angle CFE=\angle BAC=\alpha$解析① 如图，当线段 $BE$ 的长度最大时，点 $E$ 在 $BF$ 的延长线上．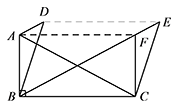
已证得四边形 $ABCF$ 是矩形，则 $\angle BFC=\angle BAC=\alpha$，
所以 $\angle BAD=\angle CFE=180^\circ-\alpha$．
② 如图，当线段 $BE$ 的长度最小时，点 $E$ 在 $BF$ 上．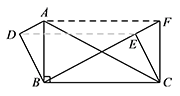
此时 $\angle BAD=\angle CFE=\angle BAC=\alpha$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
