在等边 $\triangle ABC$ 内取一点 $D$，使 $DA=DB$，在等边 $\triangle ABC$ 外取一点 $E$，使 $\angle DBE=\angle DBC$，且 $BE=BA$，求 $\angle BED$ 的度数．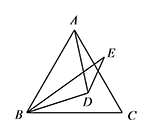
【难度】
【出处】
无
【标注】
【答案】
如图，连接 $DC$．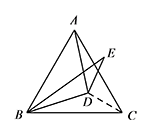
易证 $\triangle ADC \cong \triangle BDC (\rm{SSS})$，
所以 $\angle BCD=\angle ACD=\dfrac 12 ACB=30^\circ$．
由 $\angle DBE=\angle DBC$，$BE=AB=BC$，
可得 $\triangle BDE\cong \triangle BDC (\rm{SAS})$，
所以 $\angle BED=\angle BCD=30^\circ$
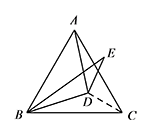易证 $\triangle ADC \cong \triangle BDC (\rm{SSS})$，所以 $\angle BCD=\angle ACD=\dfrac 12 ACB=30^\circ$．
由 $\angle DBE=\angle DBC$，$BE=AB=BC$，
可得 $\triangle BDE\cong \triangle BDC (\rm{SAS})$，
所以 $\angle BED=\angle BCD=30^\circ$
【解析】
略
答案
解析
备注
