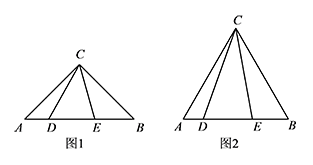
【难度】
【出处】
无
【标注】
-
如图1，在 $\mathrm {Rt}\triangle ABC$ 中，$\angle ACB=90^\circ$，$AC=BC$，点 $D,E$ 在斜边 $AB$ 上，且 $\angle DCE=45^\circ$．求证：线段 $DE,AD,EB$ 总能构成一个直角三角形．标注答案如图，将 $\triangle BCE$ 沿 $CE$ 翻折得到 $\triangle FCE$，连接 $DF$．
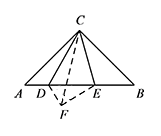则 $\angle FCE=\angle BCE$，$\angle CFE=\angle B$，$FC=BC=AC$．
而 $\angle ACD+\angle BCE=\angle FCD+\angle FCE=45^\circ$，
所以 $\angle ACD=\angle FCD$，
所以 $\triangle ACD\cong \triangle FCD (\rm{SAS})$，
从而 $\angle DFC=\angle A$，$FD=AD$，
所以 $\angle DFE=\angle DFC+\angle EFC=\angle A+\angle B=90^\circ$．
即线段 $DE,AD,EB$ 总能构成一个直角三角形解析略 -
如图2，等边 $\triangle ABC$ 中，点 $D,E$ 在边 $AB$ 上，且 $\angle DCE=30^\circ$，当 $AD$ 与 $BE$ 存在什么关系时，线段 $DE,AD,EB$ 能构成一个等腰三角形，并求出此时等腰三角形顶角的度数．标注答案如图，将 $\triangle BCE$ 沿 $CE$ 翻折得到 $\triangle FCE$，连接 $DF$．
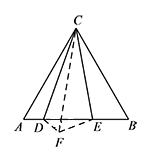则 $\angle FCE=\angle BCE$，$\angle CFE=\angle B$，$FC=BC=AC$．
而 $\angle ACD+\angle BCE=\angle FCD+\angle FCE=30^\circ$，
所以 $\angle ACD=\angle FCD$，
所以 $\triangle ACD\cong \triangle FCD (\rm{SAS})$，
从而 $\angle DFC=\angle A$，$FD=AD$，
所以 $\angle DFE=\angle DFC+\angle EFC=\angle A+\angle B=120^\circ$．
而线段 $DE,AD,EB$ 能构成的三角形为 $\triangle DFE$，
若其为等腰三角形，则只能 $FD=FE$，
所以此时 $AD=BE$．
即当 $AD=BE$ 时，线段 $DE,AD,EB$ 能构成一个等腰三角形，且此时等腰三角形顶角的度数为 $120^\circ$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
