如图,将正五边形 $ABCDE$ 绕点 $A$ 顺时针旋转 $60^\circ$ 后,旋转前后两图形有另一交点 $O$,连接 $AO$;再将 $AO$ 所在的直线绕点 $A$ 逆时针旋转 $60^\circ$ 后,交旋转前的图形于点 $P$,连接 $PO$.判断 $\triangle AOP$ 的形状,并说明理由.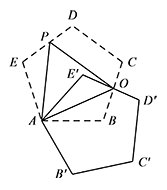
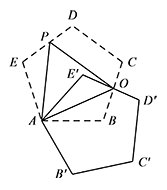
【难度】
【出处】
无
【标注】
【答案】
$\triangle AOP$ 为等边三角形
【解析】
由旋转的性质得 $\angle EAE'=\angle PAO=60^\circ$,$\angle E=\angle E'$,$AE=AE'$.
所以 $\angle EAP=\angle E'AO$,
从而 $\triangle PEA\cong \triangle OE'A (\rm{ASA})$,
所以 $AP=AO$,
即 $\triangle AOP$ 为等边三角形.
所以 $\angle EAP=\angle E'AO$,
从而 $\triangle PEA\cong \triangle OE'A (\rm{ASA})$,
所以 $AP=AO$,
即 $\triangle AOP$ 为等边三角形.
答案
解析
备注