如图所示,在菱形 $ABCD$ 中,$AC=2$,$BD=2\sqrt3$,$AC,BD$ 相交于点 $O$.将一个足够大的直角三角板 $60^\circ$ 角的顶点放在菱形 $ABCD$ 的顶点 $A$ 处,绕点 $A$ 左右旋转,其中三角板 $60^\circ$ 角的两边分别与边 $BC,CD$ 相交于点 $E,F$,连接 $EF$ 与 $AC$ 相交于点 $G$.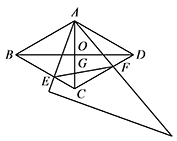
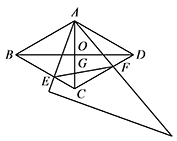
【难度】
【出处】
无
【标注】
-
判断 $\triangle AEF$ 是哪一种特殊三角形,并说明理由;标注答案$\triangle AEF$ 是等边三角形解析易得 $\angle BAE=\angle CAF$,
所以 $\triangle ABE\cong \triangle ACF (\mathrm{ASA})$,
故 $AE=AF$.
所以 $\triangle AEF$ 是等边三角形 -
旋转过程中,当点 $E$ 为边 $BC$ 的四等分点时 $\left(BE>CE\right)$,求 $CG$ 的长.标注答案$CG=\dfrac 38$解析根据题意可得 $CE=\dfrac 12$,$BE=\dfrac 32$.
所以 $CF=BE=\dfrac 32$.
因为 $\angle AEG=\angle FCG=60^\circ$,
所以 $\angle EAC=\angle GFC$.
从而 $\triangle CAE\backsim \triangle CFG$.
所以 $\dfrac{CG}{CE}=\dfrac{CF}{CA}$,
可得 $CG=\dfrac 38$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2