已知 $\triangle ABC$ 是等腰三角形，$\angle BAC=90^\circ$，$DE\perp CE$，$DE=CE=\dfrac 12 AC$，连接 $AE$，点 $M$ 是 $AE$ 的中点．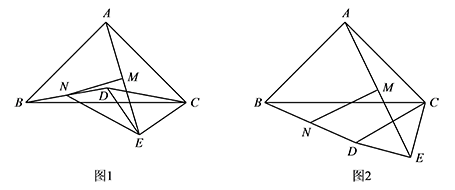
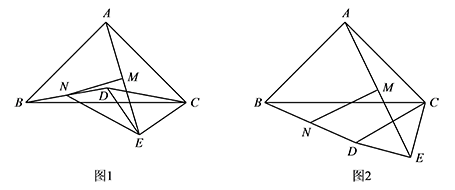
【难度】
【出处】
无
【标注】
-
如图1，若点 $D$ 在 $\triangle ABC$ 的内部，连接 $BD$，点 $N$ 是 $BD$ 中点，连接 $MN,NE$，求证：$MN\perp AE$；标注答案略解析如图，延长 $EN$ 至点 $F$，使得 $NF=NE$，连接 $FB$．
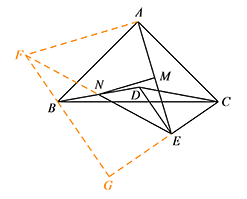易证 $\triangle DEN\cong \triangle BFN$，
从而可得 $BF\parallel DE$，$BF=DE$．
延长 $FB,CE$ 交于点 $G$，则 $\angle G=90^\circ$，
从而 $A,B,G,C$ 四点共圆，所以 $\angle ABF=\angle ACE$．
连接 $AF$，所以 $\triangle ABF\cong \triangle ACE ({\rm SAS})$．
所以 $AF=AE$，且 $AF\perp AE$．
而 $MN\parallel AF$，
所以 $MN=\dfrac 12AE$，且 $MN\perp AE$． -
如图2，将图1中的 $\triangle CDE$ 绕点 $C$ 逆时针旋转，使 $\angle BCD=30^\circ$，连接 $BD$，点 $N$ 是 $BD$ 中点，连接 $MN$，探索 $\dfrac{MN}{AC}$ 的值．标注答案$\dfrac{MN}{AC}=\dfrac {\sqrt 7}4$解析如图，同第1问可得 $MN=\dfrac 12AE$，且 $MN\perp AE$．
由题意可得 $AC=2CE$，作 $EH\perp AC$ 于点 $H$，则 $\angle ECH=60^\circ$．
所以 $CH=\dfrac 12 EC=\dfrac 14 AC$，$EH=\dfrac{\sqrt 3}4 AC$，
从而 $AE=\sqrt{AH^2+EH^2}=\dfrac{\sqrt 7}2 AC$，
所以 $\dfrac{MN}{AC}=\dfrac {\sqrt 7}4$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
