如图1，在菱形 $ABCD$ 和菱形 $BEFG$ 中，点 $A,B,E$ 在同一条直线上，$P$ 是线段 $DF$ 的中点，连接 $PG,PC$，若 $\angle ABC=\angle BEF=60^\circ$．
【难度】
【出处】
无
【标注】
-
请写出线段 $PG$ 与 $PC$ 的位置关系及 $\dfrac{PG}{PC}$ 的值；标注答案$PG\perp PC$，$\dfrac{PG}{PC}=\sqrt 3$解析延长 $GP$ 交 $CD$ 于点 $H$．
则 $\triangle PGF\cong \triangle PHD$，
所以 $PG=PH$，$DH=FG=BG$，
从而 $CH=CG$，
所以 $PG\perp PC$，$\angle PCG=\dfrac 12\angle GCH=60^\circ$，
所以 $\dfrac{PG}{PC}=\sqrt 3$． -
将图1中的菱形 $BEFG$ 绕点 $B$ 顺时针旋转，使菱形 $BEFG$ 的对角线 $BF$ 恰好与菱形 $ABCD$ 的边 $AB$ 在同一条直线上，原问题中的其他条件不变（如图2）．你在第1问中得到的两个结论是否发生变化？写出你的猜想并加以证明；标注答案第1问中的结论没有变化解析延长 $GP$ 交 $AD$ 于点 $H$，连接 $CH,CG$．
则 $\triangle PGF\cong \triangle PHD \left(\mathrm {ASA}\right)$，
所以 $PH=PG$，$HD=GF=BG$．
因为 $BF,AB$ 在同一条直线上，
所以 $\angle GBC=60^\circ=\angle HDC$．
而 $CD=CB$，
所以 $\triangle HDC\cong \triangle GBC \left(\mathrm {SAS}\right)$．
所以 $CH=CG$，$\angle DCH=\angle BCG$，
可得 $CP\perp AG$，$\angle PCG=\dfrac 12\angle HCG$．
而 $\angle HCG=\angle HCB+\angle BCG=\angle DCH+\angle HCB=120^\circ$，
所以 $\dfrac{PG}{PC}=\tan\angle PCG=\tan 60^\circ=\sqrt3$． -
若图1中 $\angle ABC=\angle BEF=2\alpha\left(0^\circ<\alpha<90^\circ\right)$，将菱形 $BEFG$ 绕点 $B$ 顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出 $\dfrac{PG}{PC}$ 的值（用含 $\alpha$ 的式子表示）．标注答案$\dfrac{PG}{PC}=\tan(90^\circ-\alpha)$解析延长 $GP$ 至点 $H$，使得 $PH=PG$，连接 $DH$ 并延长，交 $AB$ 于点 $M$．
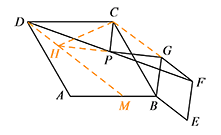则 $\triangle PGF\cong \triangle PHD$，
从而 $DM\parallel GF\parallel BE$，$DH=FG=BG$，$PH=PG$．
而 $\angle CBG+\angle ABE=\angle CDM+\angle DMB=180^\circ$，
所以 $\angle CBG=\angle CDM$．
连接 $CH,CG$，则 $\triangle CDH\cong \triangle CBG (\mathrm{SAS})$，
所以 $CH=CG$，$\angle HCG=\angle DCB=180^\circ-2\alpha$，
从而 $CP\perp PG$，$\angle PCG=\dfrac 12 \angle HCG=90^\circ-\alpha$，
所以 $\dfrac{PG}{PC}=\tan \angle PCG=\tan(90^\circ-\alpha)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
