如图1，在 $\triangle ABC$ 中，$BC=4$，以线段 $AB$ 为边作 $\triangle ABD$，使得 $AD=BD$，连接 $DC$，再以 $DC$ 为边作 $\triangle CDE$，使得 $DC=DE$，$\angle CDE=\angle ADB=\alpha$．
【难度】
【出处】
无
【标注】
-
如图2，当 $\angle ABC=45^\circ$ 且 $\alpha=90^\circ$ 时，用等式表示线段 $AD,DE$ 之间的数量关系；标注答案$AD+DE=4$解析略
-
将线段 $CB$ 沿着射线 $CE$ 的方向平移，得到线段 $EF$，连接 $BF,AF$．
（i）若 $\alpha=90^\circ$，依题意补全图 $3$，求线段 $AF$ 的长；
（ii）请直接写出线段 $AF$ 的长（用含 $\alpha$ 的式子表示）．标注答案（i）$AF=4\sqrt2$；
（ii）$AF=8\sin \dfrac{\alpha}{2}$解析（i）如图，连接 $AE$，交 $BC$ 与点 $G$，设 $DE$ 与 $BC$ 的交点为 $H$．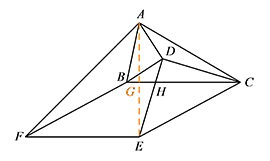
由“等腰直角三角形共顶点模型”可得 $\triangle ADE\cong \triangle BDC (\mathrm {SAS})$．
所以 $AE=BC$，$\angle EGC=\angle EDC=90^\circ$．
因为线段 $CB$ 沿着射线 $CE$ 的方向平移，得到线段 $EF$，
所以 $AE=BC=FE=4$，$AE\perp EF$．
所以 $AF=\sqrt 2EF=4\sqrt2$．
（ii）连接 $AE$，交 $BC$ 于点 $G$．
由“等腰三角形共顶点模型”中的结论可得
$FE=BC=AE$，$\angle AEF=\angle EGC=\angle EDC=\alpha$．
过点 $E$ 作 $EH\perp AF$ 于点 $H$，则 $\angle AEH=\dfrac 12 \angle AEF=\dfrac 12 \alpha$．
所以 $AF=2AH=2AE\sin\dfrac{\alpha}{2}=8\sin \dfrac{\alpha}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
