如图1,在 $\triangle ABC$ 中,$D,E$ 分别是 $AB,AC$ 上的点,且 $DE\parallel BC$,将 $\triangle ADE$ 绕 $A$ 点顺时针旋转一定角度,连接 $BD,CE$,得到图2;然后将 $BD,CE$ 分别延长至 $M,N$,使 $DM=\dfrac12 BD,EN=\dfrac12 CE$,连接 $AM,AN,MN$,得到图3.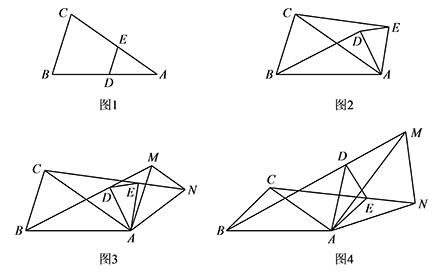
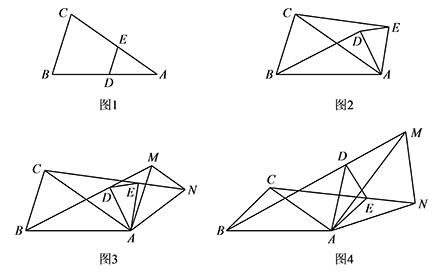
【难度】
【出处】
无
【标注】
-
若 $AB=AC$,请探究下列数量关系:
(i)在图2中,$BD$ 与 $CE$ 的数量关系是 $\underline{\qquad}$;
(ii)在图3中,猜想 $AM$ 与 $AN$ 的数量关系,$\angle MAN$ 与 $\angle BAC$ 的数量关系,并证明你的猜想;标注答案(i)$BD=CE$.
(ii)$AM=AN$,$\angle MAN=\angle BAC$解析(ii)由"等腰三角形共顶点模型"可得 $\triangle CAE\cong \triangle BAD (\mathrm {SAS})$,
所以 $CE=BD$,$\angle ACN=\angle ABM$.
所以 $BM=CN$,
从而 $\triangle ABM\cong \triangle ACN (\mathrm {SAS})$,
所以 $AM=AN$,$\angle BAM=\angle CAN$,
即 $\angle MAN=\angle BAC$. -
若 $AB=k\cdot AC\left(k>1\right)$,按上述操作方法,得到图4,请继续探究:$AM$ 与 $AN$ 的数量关系,$\angle MAN$ 与 $\angle BAC$ 的数量关系.标注答案$AM=k\cdot AN$,$\angle MAN=\angle BAC$解析由"相似三角形共顶点模型"可得 $\triangle CAE\sim \triangle BAD$,
所以 $\dfrac {BD}{CE}=\dfrac{AB}{AC}=k$,$\angle ACN=\angle ABM$.
所以 $\dfrac{BM}{CN}=\dfrac{AB}{AC}=k$,
从而 $\triangle ABM\sim \triangle ACN$,
所以 $AM=k\cdot AN$,$\angle BAM=\angle CAN$,
即 $\angle MAN=\angle BAC$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2