如图1，点 $E,F$ 分别在正方形 $ABCD$ 的边 $BC,CD$ 上，$\angle EAF=45^\circ$．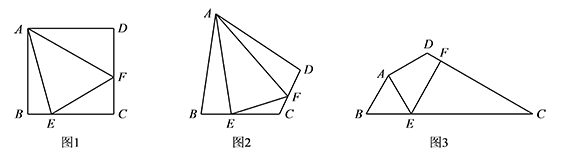
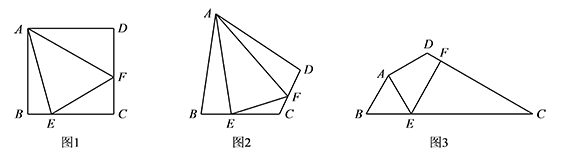
【难度】
【出处】
无
【标注】
-
试判断 $BE,EF,FD$ 之间的数量关系．标注答案$EF=BE+FD$解析由"正方形角含半角模型"即可得．
-
如图2，四边形 $ABCD$ 中，$\angle BAD\ne 90^\circ$，$AB=AD$，$\angle B+\angle D$ = $180^\circ$，点 $E,F$ 分别在边 $BC,CD$ 上，则当 $\angle EAF$ 与 $\angle BAD$ 满足 $\underline{\qquad}$ 关系时，仍有 $EF=BE+FD$．标注答案$\angle BAD=2\angle EAF$解析如图，延长 $CD$ 至点 $G$，使 $DG=BE$，连接 $AG$．
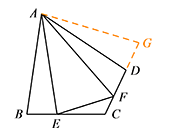易证 $\triangle ABE\cong \triangle ADG (\mathrm{SAS})$，
所以 $AE=AG$，
即 $EF=BE+DF=DG+DF=GF$．
从而证得 $\triangle AEF\cong \triangle AGF (\mathrm{SSS})$，
所以 $\angle EAF=\angle GAF=\dfrac 12 \angle EAG=\dfrac 12 \angle BAD$． -
如图3，在某公园的同一水平面上，四条通道围成四边形 $ABCD$．已知 $AB=AD=80$ 米，$\angle B=60^\circ$，$\angle ADC=120^\circ$，$\angle BAD=150^\circ$，道路 $BC,CD$ 上分别有景点 $E,F$，且 $AE\perp AD$，$DF=40(\sqrt 3-1)$ 米，现要在 $E,F$ 之间修一条笔直道路，求这条道路 $EF$ 的长．（结果取整数，参考数据：$\sqrt 2=1.41$，$\sqrt 3=1.73$）标注答案这条道路 $EF$ 的长约为 $109.2$ 米解析如图，将 $\triangle ABE$ 绕点 $A$ 逆时针旋转 $150^\circ$ 至 $\triangle ADG$，连接 $AF$．
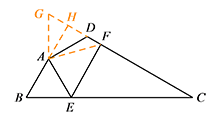由题意可得 $\angle BAE=60^\circ$，
所以 $\triangle ABE$ 和 $\triangle ADG$ 均为等边三角形．
过点 $A$ 作 $AH\perp DG$ 于点 $H$，
则 $DH=\dfrac 12AD=40 \mathrm{m}$，$AH=\dfrac{\sqrt 3}2AD=40\sqrt 3 \mathrm{m}$．
而 $DF=40(\sqrt 3-1) \mathrm m$，
所以 $AH=HF$，$\angle HAF=45^\circ$．
所以 $\angle EAF=\angle GAF=75^\circ$，
可得 $\triangle EAF\cong \triangle GAF (\mathrm{SAS})$．
所以 $EF=GF=80+40(\sqrt 3-1)\approx 109.2 \mathrm{m}$，
即这条道路 $EF$ 的长约为 $109.2$ 米．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
