如图，正方形 $ABCD$ 的边长为 $a$，$BM,DN$ 分别平分正方形的两个外角，且满足 $\angle MAN=45^\circ$，连接 $MC,NC,MN$．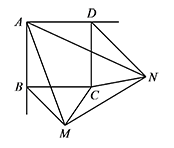
【难度】
【出处】
无
【标注】
-
与 $\triangle ABM$ 相似的三角形是 $\underline{\qquad}$，$BM\cdot DN=\underline{\qquad}$；（用含 $a$ 的代数式表示）标注答案$\triangle NDA$，$a^2$解析略
-
求 $\angle MCN$ 的度数；标注答案$\angle MCN=135^\circ$解析由第1问可得 $\dfrac{BM}{AD}=\dfrac{AB}{ND}$，
所以 $\dfrac{BM}{BC}=\dfrac{DC}{DN}$．
而易证 $\angle CBM=\angle NDC=45^\circ$，
所以 $\triangle BCM\backsim DNC$．
则 $\angle BCM=\angle DNC$，所以
$\begin{split}\angle MCN&=360^\circ-\angle BCD-\angle BCM-\angle DCN\\&=270^\circ-\left(\angle DNC+DCN\right)\\&=270^\circ-\left(180^\circ-\angle CDN\right)\\&=135^\circ.\end{split}$ -
请你猜想线段 $BM,DN$ 和 $MN$ 之间的等量关系并证明你的结论．标注答案$BM^2+DN^2=MN^2$解析如图，将 $\triangle ADN$ 绕点 $A$ 顺时针旋转 $90^\circ$ 得到 $\triangle ABE$，连接 $EM$．
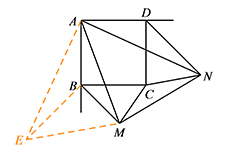易得 $AE=AN$，$\angle MAE=\angle MAN=45^\circ$，$\angle EBM=90^\circ$．
所以 $\triangle AME\cong \triangle AMN (\mathrm {SAS})$．
则 $ME=MN$．
在 $\mathrm {Rt}\triangle BME$ 中，$BM^2+BE^2=EM^2$，
所以 $BM^2+DN^2=MN^2$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
