如图，已知等边 $\triangle ABC$ 的边长为 $1$，$D$ 是 $\triangle ABC$ 外一点且 $\angle BDC=120^\circ$，$BD=CD$，$\angle MDN=60^\circ$．求 $\triangle AMN$ 的周长．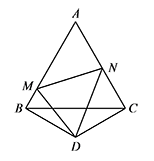
【难度】
【出处】
无
【标注】
【答案】
$\triangle AMN$ 周长为 $2$
【解析】
延长 $AC$ 到 $E$，使 $CE=BM$，连接 $DE$．
易证 $\triangle BMD\cong \triangle CED (\mathrm{SAS})$．
所以 $\angle BDM =\angle CDE$，$DM=DE$．
可得 $\angle NDE=\angle NDM=60^\circ$，
所以 $\triangle MDN\cong \triangle EDN (\mathrm{SAS})$．
从而 $MN=EN=CN+CE=CN+BM$，
所以 $\triangle AMN$ 周长为 $C_{\triangle AMN}=AB+AC=2$．
易证 $\triangle BMD\cong \triangle CED (\mathrm{SAS})$．所以 $\angle BDM =\angle CDE$，$DM=DE$．
可得 $\angle NDE=\angle NDM=60^\circ$，
所以 $\triangle MDN\cong \triangle EDN (\mathrm{SAS})$．
从而 $MN=EN=CN+CE=CN+BM$，
所以 $\triangle AMN$ 周长为 $C_{\triangle AMN}=AB+AC=2$．
答案
解析
备注
