在正方形 $ABCD$ 中，连接 $BD$，$E,F$ 是边 $BC,CD$ 上的点，$\triangle CEF$ 周长是正方形 $ABCD$ 周长的一半，$AE,AF$ 分别与 $BD$ 交于 $M,N$，试判断线段 $BM,DN,MN$ 之间数量关系，并证明．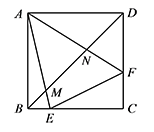
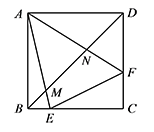
【难度】
【出处】
无
【标注】
【答案】
$BM^2+DN^2=MN^2$
【解析】
由 $\triangle CEF$ 周长是正方形 $ABCD$ 周长的一半，易想到"正方形角含半角模型"，从而通过旋转构造辅助线解决问题．
如图，延长 $CD$ 至点 $G$，使得 $DG=BE$，连接 $AG$．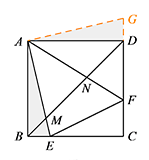
易证 $\triangle ADG\cong \triangle ABE (\rm{SAS})$，
所以 $AE=AG$，$\angle DAG=\angle BAE$，
从而 $\angle EAG=\angle BAD=90^\circ$．
由题意知 $CE+CF+EF=CB+CD=CE+CF+GF$，
所以 $EF=GF$，
所以 $\triangle AEF\cong \triangle AGF (\rm{SSS})$，
所以 $\angle EAF=\angle GAF=\dfrac 12\angle EAG=45^\circ$．
在 $AG$ 上取一点 $H$，连接 $DH,NH$．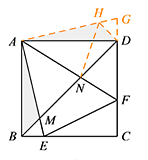
显然 $\triangle AMB\cong \triangle AHD (\rm{SAS})$，$\triangle AMN\cong \triangle AHN (\rm{SAS})$，
所以 $BM=DH$，$MN=HN$，$\angle ADH=\angle ABM=45^\circ$，
所以 $\angle HDN=90^\circ$，
从而 $BM^2+DN^2=DH^2+DN^2=HN^2=MN^2$．
如图，延长 $CD$ 至点 $G$，使得 $DG=BE$，连接 $AG$．
易证 $\triangle ADG\cong \triangle ABE (\rm{SAS})$，所以 $AE=AG$，$\angle DAG=\angle BAE$，
从而 $\angle EAG=\angle BAD=90^\circ$．
由题意知 $CE+CF+EF=CB+CD=CE+CF+GF$，
所以 $EF=GF$，
所以 $\triangle AEF\cong \triangle AGF (\rm{SSS})$，
所以 $\angle EAF=\angle GAF=\dfrac 12\angle EAG=45^\circ$．
在 $AG$ 上取一点 $H$，连接 $DH,NH$．
显然 $\triangle AMB\cong \triangle AHD (\rm{SAS})$，$\triangle AMN\cong \triangle AHN (\rm{SAS})$，所以 $BM=DH$，$MN=HN$，$\angle ADH=\angle ABM=45^\circ$，
所以 $\angle HDN=90^\circ$，
从而 $BM^2+DN^2=DH^2+DN^2=HN^2=MN^2$．
答案
解析
备注
