菱形 $ABCD$ 中，两条对角线 $AC,BD$ 相交于点 $O$，$\angle MON+\angle BCD=180^\circ$，$\angle MON$ 绕点 $O$ 旋转，射线 $OM$ 交边 $BC$ 于点 $E$，射线 $ON$ 交边 $DC$ 于点 $F$，连接 $EF$．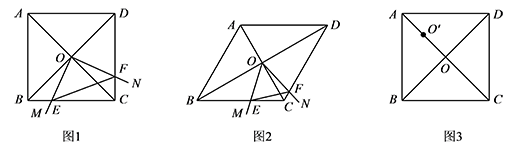
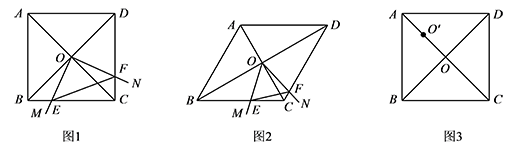
【难度】
【出处】
无
【标注】
-
如图1，当 $\angle ABC=90^\circ$ 时，$\triangle OEF$ 的形状是
-
如图2，当 $\angle ABC=60^\circ$ 时，请判断 $\triangle OEF$ 的形状，并说明理由；标注答案$\triangle OEF$ 是等边三角形解析如图，过点 $O$ 分别作 $BC,CD$ 的垂线，垂足为点 $G,H$．
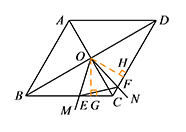易证 $\triangle EOG\cong \triangle FOH (\mathrm{ASA})$，
所以 $OE=OF$．
由已知可得 $\angle BCD=120^\circ$，
从而 $\angle MON=60^\circ$，
所以 $\triangle OEF$ 是等边三角形． -
如图3，在 $(1)$ 的条件下，将 $\angle MON$ 的顶点移动到 $AO$ 的中点 $O'$ 处，$\angle MO'N$ 绕点 $O'$ 旋转，仍满足 $\angle MO'N+\angle BCD=180^\circ$，射线 $O'M$ 交直线 $BC$ 于点 $E$，射线 $O'N$ 交直线 $CD$ 于点 $F$，当 $BC=4$，且 $\dfrac{S_{\triangle O'EF}}{S_{ 四边形 ABCD}}=\dfrac 98$ 时，求线段 $CE$ 的长．标注答案线段 $CE$ 的长为 $3\sqrt 3+3$ 或 $3\sqrt 3-3$解析如图，过点 $O'$ 分别作 $BC,CD$ 的垂线，垂足为点 $G,H$．
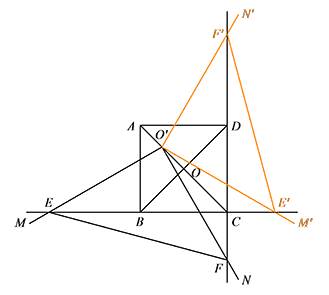易证 $\triangle EO'G\cong \triangle FO'H (\mathrm{ASA})$，
所以 $O'E=O'F$，
从而 $\triangle O'EF$ 是等腰直角三角形．
由 $\dfrac{S_{\triangle O'EF}}{S_{四边形ABCD}}=\dfrac 98$，可得 $S_{\triangle O'EF}=18$，
所以 $O'E=O'F=6$．
而 $O'G=\dfrac 34 AB=3$，所以 $EG=3\sqrt 3$．
① 当点 $E$ 在射线 $CB$ 上时，$CE=CG+EG=3\sqrt 3+3$；
② 当点 $E$ 在射线 $BC$ 上时，$CE=CG-EG=3\sqrt 3-3$．
综上，线段 $CE$ 的长为 $3\sqrt 3+3$ 或 $3\sqrt 3-3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
