如图，在 $\triangle ABC$ 中，$\angle ACB=90^\circ$，$AC=4 {\mathrm {cm}}$，$BC=3 {\mathrm {cm}}$．如果点 $P$ 由点 $B$ 出发沿 $BA$ 方向向点 $A$ 匀速运动，同时点 $Q$ 由点 $A$ 出发沿 $AC$ 方向向点 $C$ 匀速运动，它们的速度均为 $1 {\mathrm {cm}}{/}{\mathrm {s}}$．连接 $PQ$．设运动时间为 $t \mathrm {s}$（$0<t<4$），问当 $t$ 为何值时，$\triangle APQ$ 是等腰三角形？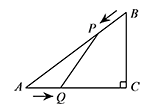
【难度】
【出处】
无
【标注】
【答案】
当 $t=\dfrac 52,\dfrac {25}{13}$ 或 $\dfrac {40}{13}$ 时，$\triangle APQ$ 是等腰三角形
【解析】
如图，过点 $P$ 作 $PH\perp AC$ 于点 $H$．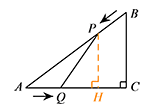
在 $\mathrm {Rt}\triangle ABC$ 中，由勾股定理得 $AB=5 {\mathrm {cm}}$．
由题意可得 $AQ=BP=t {\mathrm {cm}}$，$AP=\left(5-t\right) {\mathrm {cm}}$．
易证 $\triangle APH\sim \triangle ABC$，
所以 $\dfrac {PH}{BC}=\dfrac {AP}{AB}=\dfrac {AH}{AC}$．
所以 $PH=\dfrac {3\left(5-t\right)}{5}$，$AH=\dfrac {4\left(5-t\right)}5$．
从而 $QH=\left|\dfrac {4\left(5-t\right)} 5-t\right|=\left|4-{\dfrac {9t}5}\right|$，
所以 $PQ=\sqrt {QH^2+PH^2}=\sqrt {\left(4-\dfrac {9t} 5\right)^2+\left(\dfrac {3\left(5-t\right)} 5\right)^2}$．
① 当 $AQ=AP$ 时，即 $t=5-t$，
解得 $t_1=\dfrac 52$；
② 当 $PQ=AQ$ 时，即 ${\sqrt {\left(4-\dfrac {9t} 5\right)^2+\left(\dfrac {3\left(5-t\right)} 5\right)^2}}=t$，
解得 $t_2=\dfrac {25} {13}$，$t_3=5$；
③ 当 $PQ=AP$ 时，即 ${\sqrt {\left(4-\dfrac {9t} 5\right)^2+\left(\dfrac {3\left(5-t\right)} 5\right)^2}} =5-t$，
解得 $t_4=0$，$t_5=\dfrac {40}{13}$．
由 $0<t<4$，所以 $t_3=5$，$t_4=0$ 不合题意，舍去．
综上可得，当 $t=\dfrac 52,\dfrac {25}{13}$ 或 $\dfrac {40}{13}$ 时，$\triangle APQ$ 是等腰三角形．
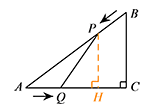在 $\mathrm {Rt}\triangle ABC$ 中，由勾股定理得 $AB=5 {\mathrm {cm}}$．由题意可得 $AQ=BP=t {\mathrm {cm}}$，$AP=\left(5-t\right) {\mathrm {cm}}$．
易证 $\triangle APH\sim \triangle ABC$，
所以 $\dfrac {PH}{BC}=\dfrac {AP}{AB}=\dfrac {AH}{AC}$．
所以 $PH=\dfrac {3\left(5-t\right)}{5}$，$AH=\dfrac {4\left(5-t\right)}5$．
从而 $QH=\left|\dfrac {4\left(5-t\right)} 5-t\right|=\left|4-{\dfrac {9t}5}\right|$，
所以 $PQ=\sqrt {QH^2+PH^2}=\sqrt {\left(4-\dfrac {9t} 5\right)^2+\left(\dfrac {3\left(5-t\right)} 5\right)^2}$．
① 当 $AQ=AP$ 时，即 $t=5-t$，
解得 $t_1=\dfrac 52$；
② 当 $PQ=AQ$ 时，即 ${\sqrt {\left(4-\dfrac {9t} 5\right)^2+\left(\dfrac {3\left(5-t\right)} 5\right)^2}}=t$，
解得 $t_2=\dfrac {25} {13}$，$t_3=5$；
③ 当 $PQ=AP$ 时，即 ${\sqrt {\left(4-\dfrac {9t} 5\right)^2+\left(\dfrac {3\left(5-t\right)} 5\right)^2}} =5-t$，
解得 $t_4=0$，$t_5=\dfrac {40}{13}$．
由 $0<t<4$，所以 $t_3=5$，$t_4=0$ 不合题意，舍去．
综上可得，当 $t=\dfrac 52,\dfrac {25}{13}$ 或 $\dfrac {40}{13}$ 时，$\triangle APQ$ 是等腰三角形．
答案
解析
备注
