如图，在平面直角坐标系中，点 $A$ 坐标为 $\left(-2,0\right)$，点 $B$ 坐标为 $\left(0,2\right)$，$E$ 为线段 $AB$ 上的动点（点 $E$ 不与点 $A,B$ 重合），以 $E$ 为顶点作 $\angle OET=45^\circ$，射线 $ET$ 交线段 $OB$ 于点 $F$，$C$ 为 $y$ 轴正半轴上一点，且 $OC=AB$，抛物线 $y=-\sqrt 2x^2+mx+n$ 的图象经过 $A,C$ 两点．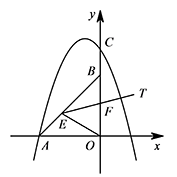
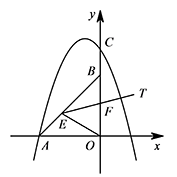
【难度】
【出处】
无
【标注】
-
求此抛物线的函数表达式；标注答案抛物线的表达式为 $y=-\sqrt 2 x^2- \sqrt 2 x+2 \sqrt 2$解析由题意可得 $OA=OB=2$，
在 $\mathrm {Rt}\triangle AOB$ 中，$AB=\sqrt {OA^2+OB^2}=2\sqrt 2$．
因为 $OC=AB $，
所以 $OC=2\sqrt 2$，即点 $C$ 的坐标为 $\left(0,2 \sqrt 2\right)$．
又抛物线 $y=-\sqrt 2 x^2+mx+n$ 的图象经过 $ A ,C $ 两点，
则有 ${\begin{cases}-4\sqrt 2-2m+n=0, \\n=2\sqrt 2, \end{cases}}$
解得 ${\begin{cases}m=-\sqrt 2, \\n=2\sqrt 2.\end{cases}}$
所以抛物线的表达式为 $y=-\sqrt 2 x^2- \sqrt 2 x+2 \sqrt 2$． -
求证：$\angle BEF=\angle AOE$；标注答案略解析因为 $OA=OB$，$\angle AOB=90^\circ$，
所以 $\angle BAO= \angle ABO=45^\circ=\angle OEF$．
又 $ \angle BEO= \angle BAO+ \angle AOE= \angle OEF+ \angle BEF $，
所以 $\angle BEF= \angle AOE$． -
当 $\triangle EOF$ 为等腰三角形时，求此时点 $E$ 的坐标．标注答案点 $E$ 坐标为 $ \left(-1,1\right) ,\left(-\sqrt 2 ,2- \sqrt 2 \right)$解析当 $\triangle EOF$ 为等腰三角形时，分三种情况讨论：
① 当 $OE=OF$ 时，$\angle OFE= \angle OEF=45^\circ$．
此时 $\angle EOF=90^\circ$，则点 $E$ 与点 $A$ 重合，不符合题意，此种情况不成立．
② 如图，当 $FE=FO$ 时，$\angle EOF= \angle OEF=45^\circ$．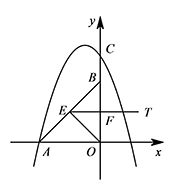
此时 $\angle EFO=90^\circ$，则 $EF\parallel AO$，
所以 $\angle BEF= \angle BAO=45^\circ$，
所以 $EF=BF=OF=\dfrac{1}{2}OB= \dfrac{1}{2} \times 2=1$，
所以点 $E$ 的坐标为 $\left(-1,1\right)$．
③ 如图，当 $EO=EF$ 时，过点 $E$ 作 $EH\perp y$ 轴于点 $H$．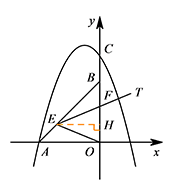
由第2问知 $\angle AOE= \angle BEF$，
所以 $\triangle AOE\cong \triangle BEF (\rm{AAS})$，
所以 $BE=AO=2$，
从而 $EH=BH=\dfrac{\sqrt 2}2BE=\sqrt 2$．
所以 $OH=OB-BH=2- \sqrt 2$，
所以点 $E$ 的坐标为 $\left(-\sqrt 2 ,2- \sqrt 2\right)$．
综上可得，当 $\triangle EOF$ 为等腰三角形时，点 $E$ 坐标为 $ \left(-1,1\right) ,\left(-\sqrt 2 ,2- \sqrt 2 \right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
