如图，抛物线 $y=-\dfrac 38x^2-\dfrac 34x+3$ 与 $x$ 轴交于 $A,B$ 两点（点 $A$ 在点 $B$ 的左侧），与 $y$ 轴交于点 $C$．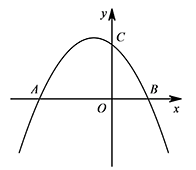
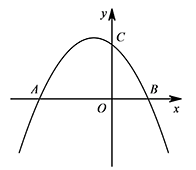
【难度】
【出处】
无
【标注】
-
求点 $A,B$ 的坐标；标注答案点 $A$ 的坐标为 $\left(-4,0\right)$，点 $B$ 的坐标为 $\left(2,0\right)$解析令 $-\dfrac 38x^2-\dfrac 34x+3=0$，
解得 $x_1=-4, x_2=2$，
所以点 $A$ 的坐标为 $\left(-4,0\right)$，点 $B$ 的坐标为 $\left(2,0\right)$． -
若直线 $l$ 过点 $E\left(4,0\right)$，$M$ 为直线 $l$ 上的动点，当以 $A,B,M$ 为顶点所作的直角三角形有且只有三个时，求直线 $l$ 的解析式．标注答案直线 $l$ 解析式为 $y=-\dfrac 34x+3$ 或 $y=\dfrac 34x-3$解析如图，以 $AB$ 为直径作 $\odot D$，过点 $E$ 作 $\odot D$ 的切线，切点为 $M_1$，则该切线即为满足题意的直线 $l$．
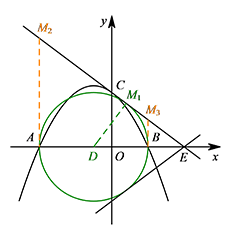过点 $A,B$ 作 $x$ 轴的垂线，分别交直线 $l$ 于点 $M_2,M_3$，则点 $M_1,M_2,M_3$ 为点 $M$ 的三种情况．
连接 $DM_1$，则 $DM_1=\dfrac 12 AB=3$．
而 $DE=\dfrac 12AB+BE=5$，从而 $M_1E=4$．
因为 $\tan \angle M_2EA=\tan \angle M_1ED=\dfrac{DM_1}{EM_1}=\dfrac 34$，
所以 $AM_2=\dfrac 34 AE=6$，即点 $M_1$ 的坐标为 $(-4,6)$．
从而求得直线 $l$ 的解析式为 $y=-\dfrac 34x+3$；
根据对称性，直线 $l$ 还可以为 $y=\dfrac 34x-3$．
综上可得，满足题意的直线 $l$ 解析式为 $y=-\dfrac 34x+3$ 或 $y=\dfrac 34x-3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
