抛物线 $y=-x^2+2x+3$ 的顶点为 $C$，点 $A$ 的坐标为 $(-1,4)$，其对称轴 $l$ 上是否存在点 $M$，使线段 $MA$ 绕点 $M$ 逆时针旋转 $90^\circ$ 得到线段 $MB$，且点 $B$ 恰好落在抛物线上？若存在，求出点 $M$ 的坐标；若不存在，请说明理由．
【难度】
【出处】
无
【标注】
【答案】
存在，点 $M$ 的坐标为 $(1,2)$ 或 $(1,5)$
【解析】
由抛物线 $y=-x^2+2x+3=-(x-1)^2+4$，
可得其顶点 $C$ 的坐标为 $(1,4)$．
如图，连接 $AC$，作 $BD\perp l$ 于点 $D$．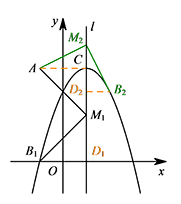
显然 $AC\perp l$，易证 $\triangle MCA\cong \triangle BDM$．
从而 $MD=AC=2$，$BD=MC$．
设点 $M$ 的坐标为 $(1,m)$．
① 当点 $A,B$ 在 $l$ 同侧时，则 $B_1D_1=M_1C=4-m$，
所以 $x_{B_1}=-(B_1D_1-x_{D_1})=m-3$，$y_{B_1}=y_{M_1}-M_1D_1=m-2$；
② 当点 $A,B$ 在 $l$ 异侧时，则 $B_2D_2=M_1C=m-4$，
所以 $x_{B_2}=B_2D_2+x_{D_2}=m-3$，$y_{B_1}=y_{M_2}-M_2D_2=m-2$．
所以无论点 $A,B$ 在 $l$ 同侧还是异侧，点 $B$ 的坐标均为 $(m-3,m-2)$．
将点 $B$ 的坐标代入抛物线解析式，可得 $-(m-3)^2+2(m-3)+3=(m-2)$，
解得 $m_1=2, m_2=5$，
综上可得，满足题意的点 $M$ 的坐标为 $(1,2)$ 或 $(1,5)$．
可得其顶点 $C$ 的坐标为 $(1,4)$．
如图，连接 $AC$，作 $BD\perp l$ 于点 $D$．
显然 $AC\perp l$，易证 $\triangle MCA\cong \triangle BDM$．从而 $MD=AC=2$，$BD=MC$．
设点 $M$ 的坐标为 $(1,m)$．
① 当点 $A,B$ 在 $l$ 同侧时，则 $B_1D_1=M_1C=4-m$，
所以 $x_{B_1}=-(B_1D_1-x_{D_1})=m-3$，$y_{B_1}=y_{M_1}-M_1D_1=m-2$；
② 当点 $A,B$ 在 $l$ 异侧时，则 $B_2D_2=M_1C=m-4$，
所以 $x_{B_2}=B_2D_2+x_{D_2}=m-3$，$y_{B_1}=y_{M_2}-M_2D_2=m-2$．
所以无论点 $A,B$ 在 $l$ 同侧还是异侧，点 $B$ 的坐标均为 $(m-3,m-2)$．
将点 $B$ 的坐标代入抛物线解析式，可得 $-(m-3)^2+2(m-3)+3=(m-2)$，
解得 $m_1=2, m_2=5$，
综上可得，满足题意的点 $M$ 的坐标为 $(1,2)$ 或 $(1,5)$．
答案
解析
备注
