如图,四边形 $ABCD$ 是直角梯形,$AD\parallel BC$,$\angle B=90^\circ$,$AD=24 {\mathrm{cm}}$,$BC=28 {\mathrm{cm}}$,点 $P$ 从点 $A$ 出发,沿 $AD$ 以 $1 {\mathrm{cm}}{/}{\mathrm{s}}$ 的速度向点 $D$ 运动;点 $Q$ 从点 $C$ 同时出发,沿 $CB$ 以 $3 {\mathrm{cm}}{/}{\mathrm{s}}$ 的速度向点 $B$ 运动,其中一个动点到达终点时,另一个点也随之停止运动.从运动开始,经过多少时间,四边形 $PQCD$ 成为平行四边形?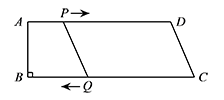
【难度】
【出处】
无
【标注】
【答案】
经过 $6 {\mathrm{s}}$ 四边形 $PQCD$ 成为平行四边形
【解析】
由已知可得 $AP=t$,$PD=24-t$,$CQ=3t$.
若四边形 $ PQCD $ 是平行四边形,
那么 $PD=QC $,即 $24-t=3t$,
解得 $t=6<\dfrac {28}3$.
所以经过 $6 {\mathrm{s}}$ 四边形 $PQCD$ 成为平行四边形.
若四边形 $ PQCD $ 是平行四边形,
那么 $PD=QC $,即 $24-t=3t$,
解得 $t=6<\dfrac {28}3$.
所以经过 $6 {\mathrm{s}}$ 四边形 $PQCD$ 成为平行四边形.
答案
解析
备注