已知抛物线 $y=a(x-1)^2-\dfrac{25}{3}$ 与 $x$ 轴交于 $A,B$ 两点（点 $A$ 在点 $B$ 左边），且过点 $D\left(5,-3\right)$，顶点为 $M$，直线 $MD$ 交 $x$ 轴于点 $F$．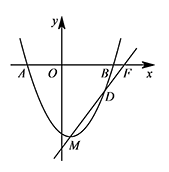
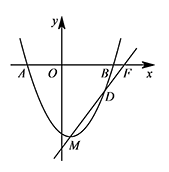
【难度】
【出处】
无
【标注】
-
求 $a$ 的值和 $M$ 点的坐标；标注答案$M(1,-\dfrac{25}{3})$，，$a=\dfrac13$解析由抛物线解析式可得 $M(1,-\dfrac{25}{3})$；
把 $D(5,-3)$ 代入 $y=a(x-1)^2-\dfrac{25}{3}$，得 $a=\dfrac13$． -
以 $AB$ 为直径画 $\odot P$，问：点 $D$ 在 $\odot P$ 上吗，为什么？标注答案点 $D$ 在 $\odot P$ 上解析令 $y=0$，则 $\dfrac13(x-1)^2-\dfrac{25}{3}=0$，
解得 $x_1=-4$，$x_2=6$．
所以 $A(-4,0), B(6,0), P(1,0)$，且 $\odot P$ 的半径 $r=5$．
过点 $D$ 作 $DE\perp x$ 轴于点 $E$，则 $E(5,0)$，连接 $DP$．
在 $\mathrm{Rt}\triangle DEP$ 中，
由勾股定理可得 $PD=\sqrt{PE^2+DE^2}=5=r$．
所以点 $D$ 在 $\odot P$ 上． -
直线 $MD$ 与 $\odot P$ 存在怎样的位置关系？请说明理由．标注答案点 $D$ 在 $\odot P$ 上，所以直线 $MD$ 与 $\odot P$ 相切解析设直线 $MD$ 的函数解析式为 $y=kx+b (k\ne 0)$，
把 $M(1,-\dfrac{25}{3}),D(5,-3)$ 代入得
$\begin{cases}-\dfrac{25}{3}=k+b,\\-3=5k+b,\end{cases}$ 解得 $\begin{cases}k=\dfrac43,\\b=-\dfrac{29}{3}.\end{cases}$
所以直线 $MD$ 的函数解析式为 $y=\dfrac43x-\dfrac{29}{3}.$
令 $y=0$，则 $0=\dfrac43x-\dfrac{29}{3}$，
得 $x=\dfrac{29}{4}$，所以 $F\left(\dfrac{29}{4},0\right)$．
因为 $DF^2=EF^2+DE^2=\dfrac{225}{16}$，$PF^2=\left(\dfrac{29}{4}-1\right)^2=\dfrac{625}{16}$，$DP^2=25$，
所以 $DP^2+DF^2=PF^2$，
则 $FD\perp DP$．
而点 $D$ 在 $\odot P$ 上，所以直线 $MD$ 与 $\odot P$ 相切
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
