在平面直角坐标系 $xOy$ 中，抛物线 $y=ax^2+bx+c$ 交 $x$ 轴于 $A,B$ 两点，交 $y$ 轴于点 $C$，已知抛物线的对称轴为 $x=1$，$B(3,0)$，$C(0,-3)$．
【难度】
【出处】
无
【标注】
-
求抛物线的解析式；标注答案$y=\left(x-1\right)^2-4=x^2-2x-3$解析设抛物线的解析式为 $y=a\left(x-1\right)^2+k$，
将点 $B(3,0),C(0,-3)$ 代入得 $ a=1,k=-4$．
所以抛物线的解析式为 $y=\left(x-1\right)^2-4=x^2-2x-3$． -
平行于 $x$ 轴的一条直线交抛物线于 $M,N$ 两点，若以 $MN$ 为直径的圆恰好与 $x$ 轴相切，求此圆的半径．标注答案$\dfrac{-1+\sqrt{17}}{2}$ 或 $\dfrac{1+\sqrt{17}}{2}$解析令点 $M$ 在点 $N$ 的左侧，设圆的半径为 $r$，
则 $x_N=r+1,y_N=(r+1-1)^2-4=r^2-4$．
若以 $MN$ 为直径的圆与 $x$ 轴相切，则 $\lvert r^2-4 \rvert=r$，
解得 $r_1=\dfrac{1+\sqrt{17}}{2}, r_2=\dfrac{-1+\sqrt{17}}{2}$．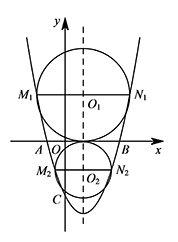
如图所示，满足条件的圆有两个，其半径为 $\dfrac{-1+\sqrt{17}}{2}$ 或 $\dfrac{1+\sqrt{17}}{2}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
