如图，已知直线 $y=\dfrac 12x$ 与双曲线 $y=\dfrac kx$（$k>0$）交于 $A,B$ 两点，且点 $A$ 的横坐标为 $4$．
【难度】
【出处】
无
【标注】
-
求 $k$ 的值．标注答案$k=8$解析因为点 $A$ 的横坐标为 $4$，所以点 $A$ 的坐标为 $\left(4,2\right)$．
因为点 $A$ 是直线 $y=\dfrac 12x$ 与双曲线 $y=\dfrac kx$（$k>0$）的交点，
所以 $k=8$． -
若双曲线 $y=\dfrac kx (k>0)$ 上一点 $C$ 的纵坐标为 $8$，求 $\triangle AOC$ 的面积．标注答案$15$解析如图，因为点 $C$ 在双曲线上，所以 $C$ 点坐标是 $\left(1,8\right)$．
过点 $A,C$ 分别作 $x$ 轴、$y$ 轴的垂线交点为 $D$，垂足为 $M,N$，
得到矩形 $ONDM$．
所以 $D\left(4,8\right), N\left(0,8\right), M\left(4,0\right)$，
所以 $S_{ \text{矩形} ONDM}=32, S_{\triangle ONC}=4, S_{\triangle CDA}=9, S_{\triangle OAM}=4$，
所以 $S_{\triangle AOC}=S_{ \text{矩形} ONDM}-S_{\triangle ONC}-S_{\triangle CDA}-S_{\triangle OAM}=15$． -
过原点 $O$ 的另一条直线 $l$ 交双曲线 $y=\dfrac kx$（$k>0$）于 $P,Q$ 两点（$P$ 点在第一象限），若由 $A,B,P,Q$ 为顶点组成的四边形面积为 $24$，求点 $P$ 的坐标．标注答案点 $P$ 的坐标为 $\left(2,4\right)$ 或 $\left(8,1\right)$解析根据反比例函数的性质可得，$OA=OB$，$OP=OQ$，
所以以 $A,P,B,Q$ 四点为顶点的四边形构成平行四边形．
设 $P\left(m,\dfrac 8m\right)$，
分别过点 $P$，$A$ 作 $x$ 轴的垂线，垂足为点 $E$，$F$，
① 如图，当 $0<m<4$ 时，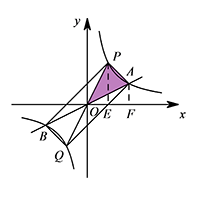
因为 $S_{\triangle POE}+S_{ \text{梯形} PEFA}=S_{\triangle POA}+S_{\triangle AOF}$，且 $S_{\triangle POE}=S_{\triangle AOF}$，
所以 $S_{ \text{梯形} PEFA}=S_{\triangle POA}=6$，
所以 $\dfrac 12\left(2+\dfrac 8m\right)\cdot \left(4-m\right)=6$，
解得 $m=2 $ 或 $m=-8 $（舍去），
所以点 $P$ 的坐标为 $\left(2,4\right)$．
② 如图，当 $m>4$ 时，
因为 $S_{\triangle AOF}+S_{ \text{梯形} AFEP}=S_{\triangle AOP}+S_{\triangle POE}$，
所以 $S_{ \text{梯形} PEFA}=S_{\triangle POA}=6$，
所以 $\dfrac 12\left(2+\dfrac 8m\right)\cdot \left(m-4\right)=6$，
解得 $m=8$ 或 $m=-2$（舍去），
所以点 $P$ 的坐标为 $\left(8,1\right)$．
综上所述，四边形的面积为 $24$ 时，点 $P$ 的坐标为 $\left(2,4\right)$ 或 $\left(8,1\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
