已知过原点的动直线 $l$ 与圆 $C_1:x^2+y^2-6x+5=0$ 相交于不同的两点 $A,B$．
【难度】
【出处】
2015年高考广东卷（文）
【标注】
-
求圆 $C_1$ 的圆心坐标；标注答案$(3,0)$解析圆 $C_1$ 的标准方程为 $C_1:(x-3)^2+y^2=4$，因此圆 $C_1$ 的圆心坐标为 $(3,0)$．
-
求线段 $AB$ 的中点 $M$ 的轨迹 $C$ 的方程；标注答案$x^2-3x+y^2=0 \left(\dfrac 53 < x\leqslant 3\right)$解析由垂径定理知 $AB\perp C_1M$，因此 $\angle OMC_1$ 始终为直角，于是 $M$ 的轨迹是以 $OC_1$ 为直径的圆在圆 $C_1$ 内（不包含交点）的部分，如图．
设以 $OC_1$ 为直径的圆为圆 $C$，则$$C:x(x-3)+y^2=0.$$联立圆 $C$ 的方程与圆 $C_1$ 的方程，可得它们的交点坐标为 $P\left(\dfrac 53,\dfrac{2\sqrt 5}3\right)$，$Q\left(\dfrac 53,-\dfrac{2\sqrt 5}3\right)$，因此所求的轨迹方程为$$x^2-3x+y^2=0 \left(\dfrac 53 < x\leqslant 3\right).$$ -
是否存在实数 $k$ 使得直线 $L:y=k(x-4)$ 与曲线 $C$ 只有一个公共点？若存在，求出 $k$ 的取值范围；若不存在，说明理由．标注答案$\left[-\dfrac{2\sqrt 5}7,\dfrac{2\sqrt 5}7\right]\cup\left\{\dfrac 34,-\dfrac 34\right\}$解析设 $N(4,0)$，过 $N$ 作圆 $C$ 的切线 $y=m(x-4)$．
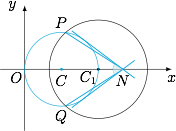由$$\dfrac{\left|\dfrac 32m-4m\right|}{\sqrt{1+m^2}}=\dfrac 32,$$解得 $m=\pm \dfrac 34$．
而直线 $NQ$，$NP$ 的斜率为 $\pm\dfrac{2\sqrt 5}7$，因此 $k$ 的取值范围是 $\left[-\dfrac{2\sqrt 5}7,\dfrac{2\sqrt 5}7\right]\cup\left\{\dfrac 34,-\dfrac 34\right\}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
