如图,在三棱锥 中,$AC = BC = 2$,$\angle ACB = {90^ \circ }$,侧面 $PAB$ 为等边三角形,侧棱 $PC = 2\sqrt 2 $,$E$ 为 $PB$ 中点.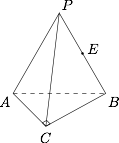

【难度】
【出处】
2011年南京理工大学自主招生暨保送生考试数学试题
【标注】
-
求证:$PC\perp AB$;标注答案略解析取 $AB$ 的中点 $H$,连接 $PH$、$CH$,则 $PH \perp AB$,$CH \perp AB$,所以 $AB \perp\text{平面} PHC$,
因此 $AB \perp PC$.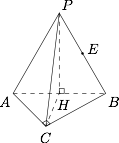
-
求证:平面 $PAB \perp $ 平面 $ABC$;标注答案略解析$PH = \dfrac{{\sqrt 3 }}{2}AB = \sqrt 6 $,$CH = \sqrt 2 $,$PC = 2\sqrt 2 $,所以 $\triangle PHC$ 为直角三角形,$PH \perp HC$.
因此 $PH \perp ABC$,于是 $PAB \perp ABC$. -
求点 $E$ 到平面 $PAC$ 的距离.标注答案$\dfrac{\sqrt {42}}{7}$解析因为 $PE=EB$,所以 $d(E,PAC)=\dfrac 12d(B,PAC)$.
在 $\triangle PAC$ 中,$PA = 2\sqrt 2 $,$PC = 2\sqrt 2 $,$AC = 2$,所以 ${S_{\triangle PAC}} = \sqrt 7 $.考虑$$V_{P-ABC}=\dfrac 13\cdot\dfrac 12\cdot 2\cdot 2\cdot\sqrt 6=\dfrac 13\cdot\sqrt 7\cdot d(B,PAC),$$解得 $d(B,PAC)=\dfrac 27\sqrt{42}$.所以 $d\left( {E, PAC} \right) =\dfrac{\sqrt {42}}{7}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3